Min Heap Algorithm

Min Heap Algorithm

Written by Richa Kiran on Dec 2nd, 2021 ・ Views ・ Report Post

Richa Kiran Visit User Profile

A heap is a Complete Binary Tree having its nodes or elements in an ordered way. Based on this order, we define two types of Heap data structures - Min Heaps and Max Heaps. In this tutorial, we're gonna see how you can call "Heapify" on a complete binary tree to change it from a common complete binary tree to a Min Heap.

What is "Heapify"?

Heapify is a method of converting a set of values into a heap. The logic behind the heapify algorithm will determine which type of heap the set of values will become.

In my previous tutorial, we discussed about the algorithm that would help us convert an array of values into a Complete Binary Tree. All we have to do now, is to call "Heapify" on the already generated complete binary tree to convert it into a heap. Let's get started!

Min Heap

Let's start with the algorithm associated with a "Min Heap". Firstly we should know what a Min Heap is to implement it in our program.

What is a Min Heap?

It is a Complete Binary Tree containing the smallest value in the root node, followed by larger values in the next level, followed by even bigger values in the next level and so on. So, the last level of this binary tree should contain the largest values present in the array of values that we're inserting.

It looks something like this - min-heap-create.gif

The Algorithm

To start with the algorithm, we first have to iterate to the rightmost parent Node in the complete binary tree and then start the comparison process from that node.

The Algorithm to reach the right most parent node is as follows -

  1. Check if the root node is NULL or not.
    1. If it is - return root itself
    2. If not - do the following :
      1. check if the root node has a right child.
        1. if it does - recurse over the right subtree over and over until the rightmost parent node is found.
        2. If it doesn't - check if it has a left child node.
          1. If it does - it means, it is the right most parent node of the tree and so return the node itself.
          2. If it doesn't - return it's parent node as that would be the right most parent node in that case.

Note that I added an extra "parent" element inside the NODE structure for easier traversal between the parent and child nodes. Without it, the movement between them is almost impossible. Likewise, I made some changes in the insertion function so that the parent element serves it's purpose in the NODE data structure we created.

🤩 Our Amazing Sponsors 👇
DigitalOcean View Website
DigitalOcean offers a simple and reliable cloud hosting solution that enables developers to get their website or application up and running quickly.
Laravel News View Website
Laravel News keeps you up to date with everything Laravel. Everything from framework news to new community packages, Laravel tutorials, and more.
Genesis View Website
A Laravel Starter Kit that includes Authentication, User Dashboard, Edit Profile, and a set of UI Components.

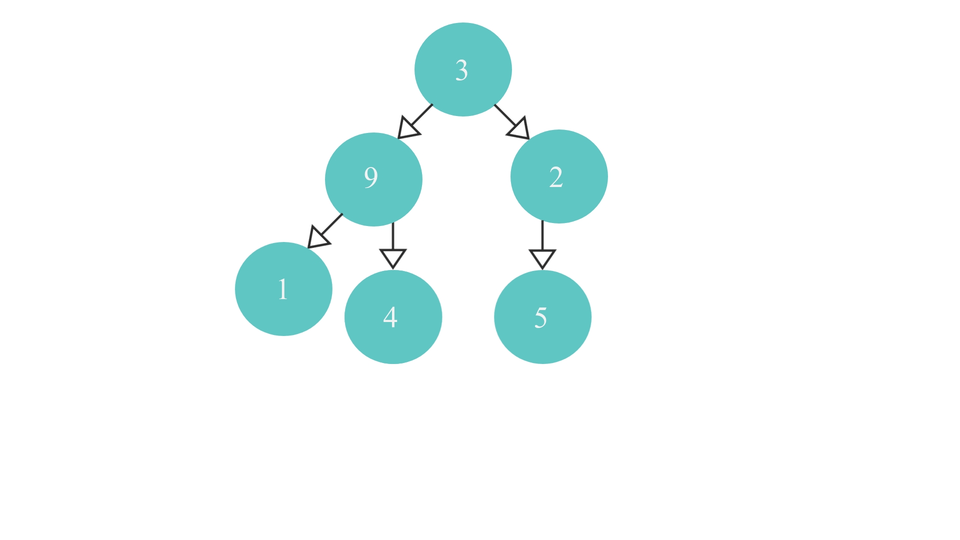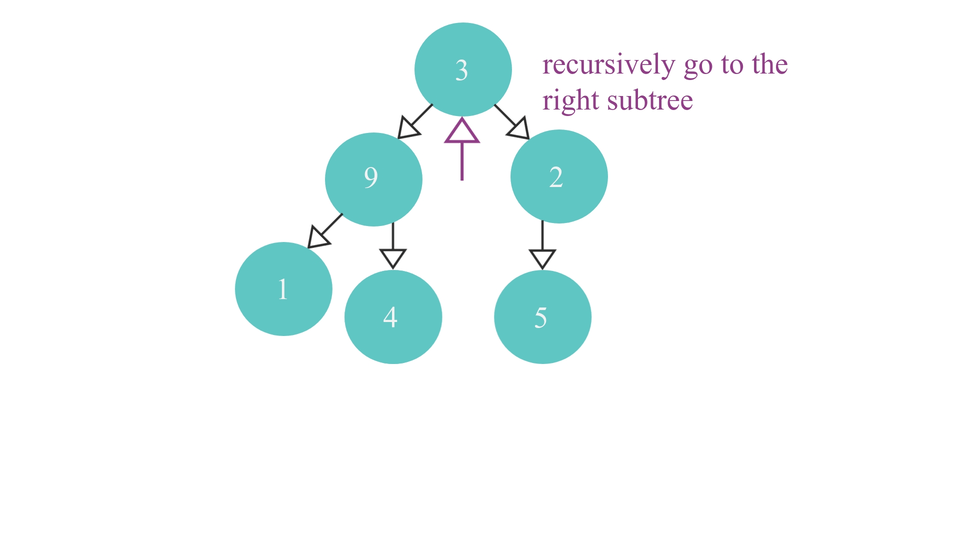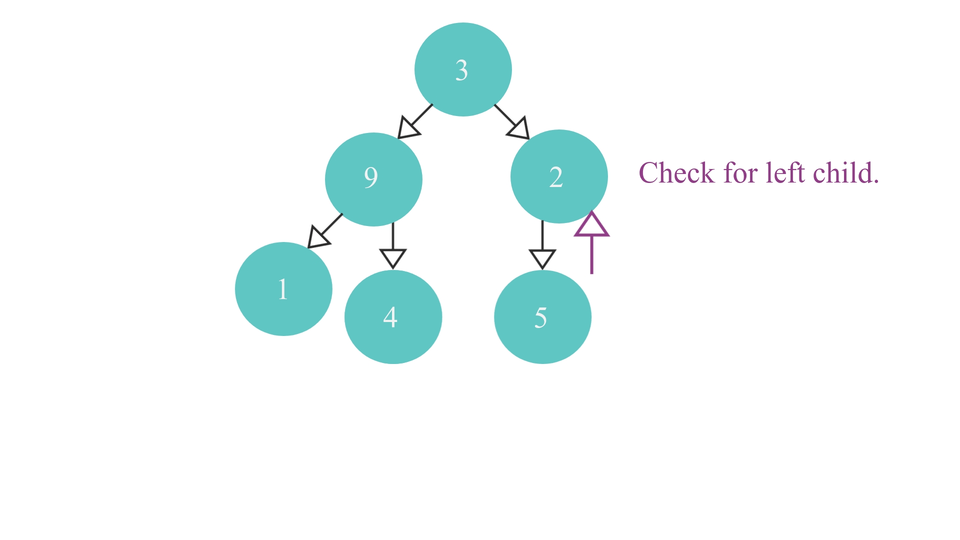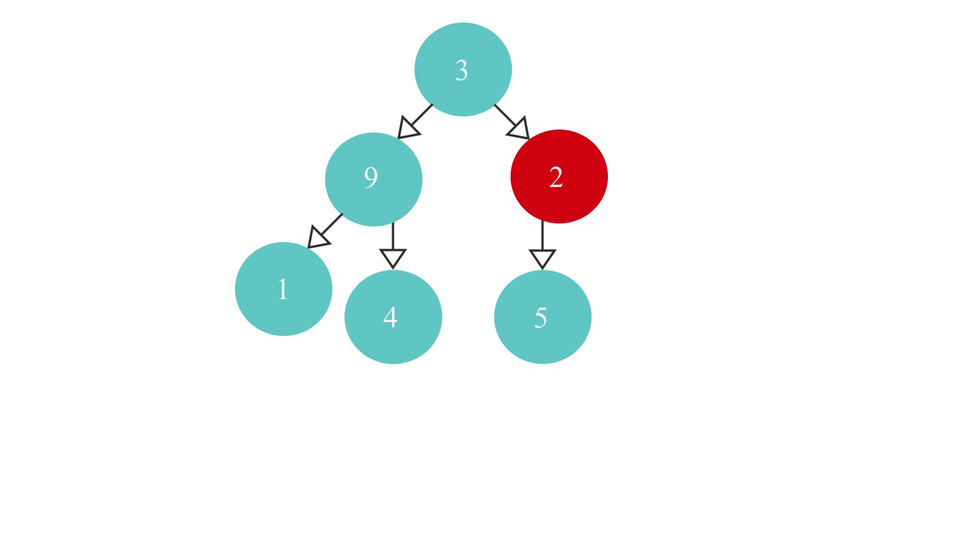
So the process looks like this - reachRight.gif

The code to reach the right most parent node is as follows -

NODE *reachRight(NODE *root){
    if(root == NULL){
        return root;
    }else{
        if(root->right==NULL){
            //check if it has left child
            if(root->left == NULL){
                //node doesnt have a left AND a right child
                //return Parent node
                return root->parent;
            }else{
                //just return the current node as it is not a leaf node
                return root;
            }
        }else{
            return reachRight(root->right);
        }
    }
}

Now that we know how to reach the right most node, let's start with the comparison process which is the main heapify code.

Heapify Algorithm

  1. Find the right most parent node(let's call it "rmp") of the tree using the above function.
  2. Check if rmp has a right child node. In either case left child node would definitely be there as in either cases rmp is a "parent" node. So, compare rmp's data with its child node's data. If the child node's value is smaller than rmp's value, swap their values(for a max heap, do the opposite - swap values is child nodes have value greater than rmp).
  3. Now, check if rmp's parent is NULL or not.
    1. If it is NULL, it means that rmp is actually pointing to the root node as no other node in a tree can't have a parent node. To mark this visit to the root node, we'll take a global variable(let's say count) initially equal to 0. Check if the value of count is equal 0 or not.
      1. If it is equal to 0, it means that root node is being visited for the first time. In that case, increment the count by 1. Find the right most parent of rmp's(or root's) left subtree and then call heapify(this function) recursively with left subtree's rmp as its argument.
      2. If not equal to 0, it means that root node was already visited before, so just return the root node(or rmp) itself.
    2. If it is not NULL, then rmp is not the root node. So, first check if rmp is right child or the left child of its parent node.
      1. If it is the right child, then call heapify(this function) on the left child of it's parent node so that comparison process can be done spread on to the left child.
      2. If it is the left child, then call heapify(this function) on the parent node itself for carrying out the comparison on the upper part of the tree.

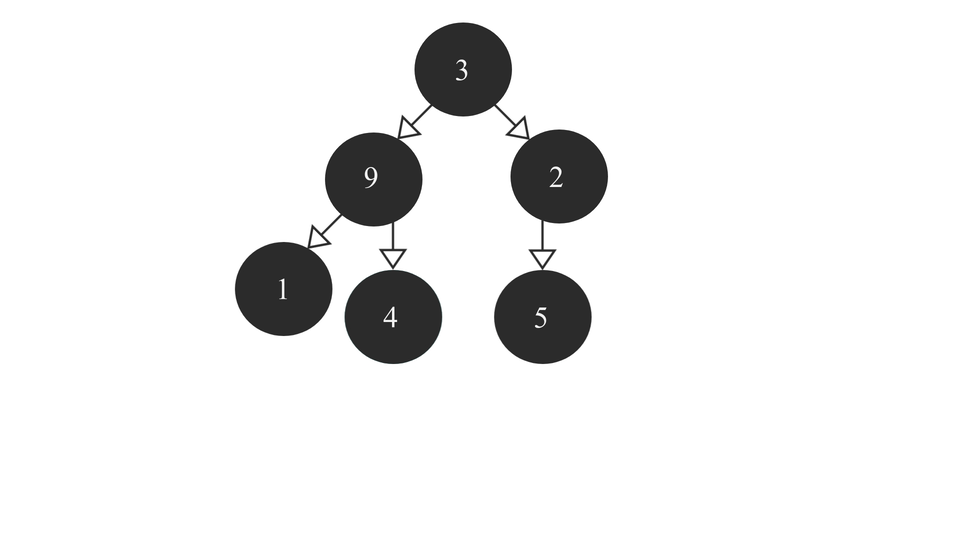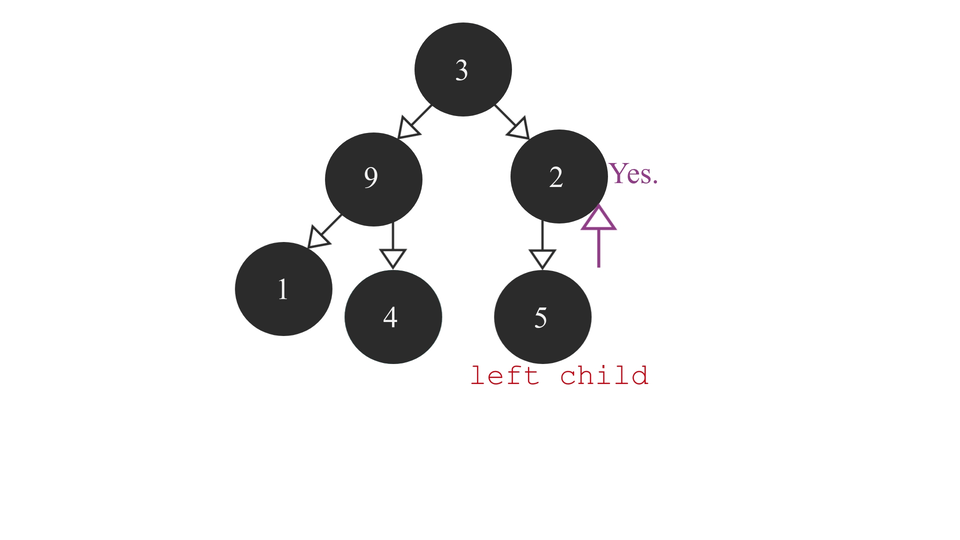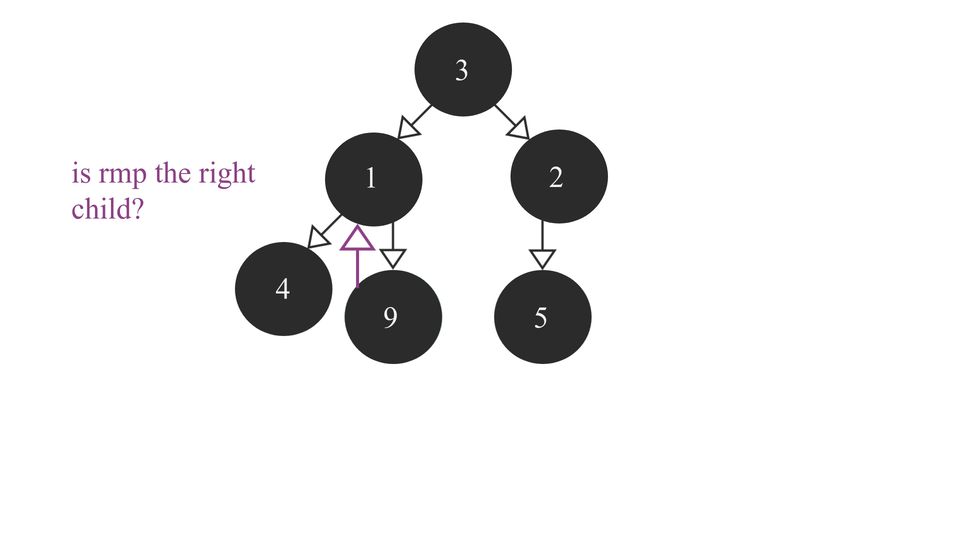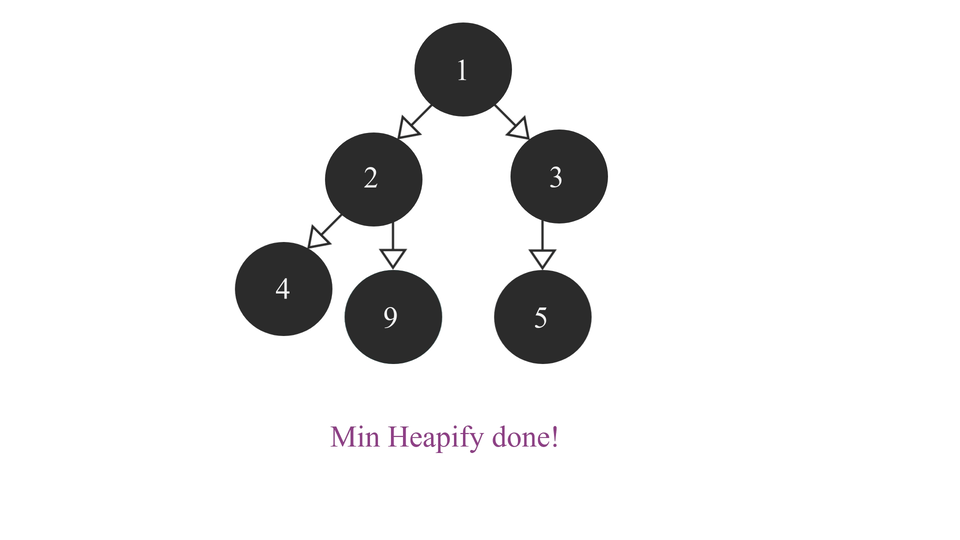
Practically, the process would look something like this - minHeap.gif

The code for Heapify function

The code for it is as follows -

void *heapify(NODE *rmp){
    int temp;
    //check for children of rmp;
    if(rmp->right == NULL){
        //it has only the left child.
        //compare value with the left child
        if(rmp->data > rmp->left->data){//check with the left child value
            temp = rmp->data;
            rmp->data = rmp->left->data;
            rmp->left->data = temp;
        }
    }else{
        //it has both the children
        //compare values with both children
        if(rmp->data > rmp->right->data){//check with the right child value
            temp = rmp->data;
            rmp->data = rmp->right->data;
            rmp->right->data = temp;
        }
        if(rmp->data > rmp->left->data){//check with the left child value
            temp = rmp->data;
            rmp->data = rmp->left->data;
            rmp->left->data = temp;
        }
    }
    if(rmp->parent==NULL){ //rmp is the root node
        if(count == 0){
            //root node is being visited for the first time
            NODE *rmpLeft = reachRight(rmp->left);
            count++;
            return heapify(rmpLeft);
        }else{
            //root node is being visited for the last time
            return rmp;
        }
    }else{// if rmp is not root node
        //first iterate over the left child of rmp's parent
        if(rmp == rmp->parent->right){
            return heapify(rmp->parent->left);
        }else{
            return heapify(rmp->parent);
        }
    }
}

Note that you just need to simply switch the comparison signs to transform this min heap algorithm to a max heap algorithm.

Full code

#include <stdio.h>
#include <stdlib.h>

typedef struct node{
    int data;
    struct node *left;
    struct node *right;
    struct node *parent;
}NODE;

NODE *rootNode = NULL;
int count = 0;
NODE *createnode(int val){
    NODE *newnode = (NODE *)malloc(sizeof(NODE));
    newnode->data = val;
    newnode->left = NULL;
    newnode->right = NULL;
    newnode->parent = NULL;
    return newnode;
}

NODE *insertInTree(int val, NODE *root){
    NODE *newnode = createnode(val);
    if(root == NULL){
        root = rootNode = newnode;
    }else{
        if(root->left == NULL){
            root->left = newnode;
            newnode->parent = root;
        }else{
            if(root->right == NULL){
                root->right = newnode;
                newnode->parent = root;
            }else{
                if(root->left->left==NULL || root->left->right==NULL){
                    return insertInTree(val, root->left);
                }else if(root->right->left==NULL || root->right->right==NULL){
                    return insertInTree(val, root->right);
                }else{
                    return insertInTree(val, root->left->left);
                }
            }
        }
    }
    return root;
}

NODE *reachRight(NODE *root){
    if(root == NULL){
        return root;
    }else{
        if(root->right==NULL){
            //check if it has left child
            if(root->left == NULL){
                //node doesnt have a left AND a right child
                //return Parent node
                return root->parent;
            }else{
                //just return the current node as it is not a leaf node
                //it has a left child
                return root;
            }
        }else{
            //it has both children
            return reachRight(root->right);
        }
    }
}

void inorder(NODE *root){
    if(root == NULL){
        return;
    }else{
        inorder(root->left);
        printf("%d ", root->data);
        inorder(root->right);
    }
}

void *heapify(NODE *rmp){
    int temp;
    //check for children of rmp;
    if(rmp->right == NULL){
        //it has only the left child.
        //compare value with the left child
        if(rmp->data > rmp->left->data){//check with the left child value
            temp = rmp->data;
            rmp->data = rmp->left->data;
            rmp->left->data = temp;
        }
    }else{
        //it has both the children
        //compare values with both children
        if(rmp->data > rmp->right->data){//check with the right child value
            temp = rmp->data;
            rmp->data = rmp->right->data;
            rmp->right->data = temp;
        }
        if(rmp->data > rmp->left->data){//check with the left child value
            temp = rmp->data;
            rmp->data = rmp->left->data;
            rmp->left->data = temp;
        }
    }
    if(rmp->parent==NULL){ //rmp is the root node
        if(count == 0){
            //root node is being visited for the first time
            NODE *rmpLeft = reachRight(rmp->left);
            count++;
            return heapify(rmpLeft);
        }else{
            //root node is being visited for the last time
            return rmp;
        }
    }else{// if rmp is not root node
        //first iterate over the left child of rmp's parent
        if(rmp == rmp->parent->right){
            return heapify(rmp->parent->left);
        }else{
            return heapify(rmp->parent);
        }
    }
}

int main(){
    //Insert
    int arr[6] = {3,9,2,1,4,5};
    for(int i=0; i<6; i++){
     insertInTree(arr[i], rootNode);   
    }
              
    printf("Inorder Traversal before: ");
    inorder(rootNode);
    printf("\n\n");
    
    NODE *rmp = reachRight(rootNode);
    heapify(rmp);
    
    printf("\nInorder Traversal after: ");
    inorder(rootNode);
    
}

Conclusion

It is very important to know that even though we say that heaps are complete binary trees, we dont normally use heapify on an actual binary tree while implementing it. We make use of arrays for that purpose. It is the ideal method for heapify as it is easy to understand, the time complexity is considerably reduced and it is not as lengthy as the code that we came across in this article. I used this method to introduce heapify as it is better to visualize the process once you get the gist of it.

I hope you liked reading this article. For more such articles, click here.

Thanks for reading!🎆

Comments (0)