During our school days, we were frequently taught how to compute the GCD. However, in terms of programming, it is currently a task that assists many complex algorithms in processing the findings. For Example - A large software that suggests the space for different dimensions for distribution. To arrange something in the group, In Measurement and Construction fields, etc. If you are new to programming, you may have been asked to write a variety of basic mathematics-related tasks. One of them is GCD. Finally, if you are conducting competitive programming, there are many questions where the solution may be dependent on the GCD of two integers. However, in this scenario, a faster technique is required to ensure that all test cases are completed. In this post, we'll look at how to write a Java Program that computes the GCD of two integers. But, before we get to the answer, let's refresh and broaden our understanding of GCD.
What is GCD?
GCD or the Greatest Common Divisor. It is a mathematical technique for determining the biggest integer that can be divided by two given any other number. The GCD is just the product of the split numbers, and it is a highly important tool for identifying the smallest amount of integers that must be considered while conducting a computation. The GCD is also known as the Highest Common Factor (HCF).
Example 1: Two numbers, 64 and 24, are provided. The highest number that can entirely divide both the numbers is 8. Explanation: The numbers that may be used to divide 64 and 24 are [1, 2, 4, 8]. The biggest number among these is 8.
Example 2: Two numbers, 176 and 96, are provided. The highest number that can entirely divide both of the numbers is 16. Explanation: The numbers that may be used to divide 96 and 176 are [1, 2, 4, 6, 8, 16]. The biggest number among these is 16.
How to calculate the GCD of Two Numbers in Java
We may deduce from the instances above that the biggest number that can divide both numbers is smaller than the lowest number between both of the input numbers. So we may devise a naive approach in which we check each number starting with the smallest number between the two integers and working our way up to 1. So the GCD of the two numbers will be whichever number arrives first and that completely divides both of the input numbers.
Example - Two Number: A = 96 & B = 176 Smallest Number: A = 96 So the iteration will begin at 96 and end at 1. Then we'll discover that the first number that entirely divides both integers (96 and 176) is 16. So, as a result, 16 will be the GCD of 96 and 176.
The algorithm that follows the above approach for finding GCD is - Initialize the 2 numbers as input from the user in number1 and number2 variables. Find the minimum number between the two input numbers and store it in a variable (minNumber). Initialize a loop starting from minNumber and going to 1. Check if the input numbers are divisible by the current iterating number. If yes then store it in a result and break out of the loop otherwise continue the next iteration. Print the result.
Java Program for the above algorithm is -
import java.util.Scanner;
class InterviewBit {
public static void main(String args[]) {
//Scanner class helps accepting user inputs. So accepting
//and storing in variables.
Scanner sc = new Scanner(System.in);
int number1 = sc.nextInt();
int number2 = sc.nextInt();
int result = 1;
//Calculating the smallest number between 2 inputs.
int small = Math.min(number1, number2);
//Iteration from small to 1.
for(int i = small; i > 0; i--){
//The first number we get that completely divides
//then store in result and come out of loop.
if(number1 % i == 0 && number2 % i == 0){
result = i;
break;
}
}
//Printing the result.
System.out.println("GCD of "+number1+" and "+number2+" is = "+result);
}
}
Run this Code on InterviewBit
 View Website
View Website
 View Website
View Website
 View Website
View Website
Input - 176 96
Output - GCD of 176 and 96 = 16.
Explanation - The smallest number is 96 since the iteration begins with 96 and checks to see whether it can completely divide both of the input numbers. 96 does not divide both integers in this iteration. So on to the next number, 95. This number also does not divide the input numbers, therefore the iteration process continues. When it reaches 16, it discovers that 16 can divide both of the input numbers. So it stores the number in the result and ends the loop. Then it prints the result.
Algorithm Analysis - In the worst-case scenario, the loop loops from the smallest integer from input to 1. So the time complexity will be O(n). And for space, it is not taking up any additional space, except for constant variable independent of the input. So as a result, the space complexity will always be O(1).
After analyzing the above algorithm, we can observe that the time complexity is O(n), which is inefficient. As a result, we can lower the algorithm's complexity.
So, in the above example, we can see that the loop goes from 96 to 16. This is a pointless check. So, we may use part of the iterations to see if the lowest number can divide the largest number. If it can, then that is the GCD. otherwise, the number that can divide both will be less than half of the smallest number. So we may check for this and begin iteration with half of the least value.
Let's look at an example to better grasp this -
A = 176 and B = 96 are two numbers. 96 cannot be divided by 176 in this circumstance. So the next integer that can divide both will undoubtedly be smaller than (96/2 = 48). Because integers between 48 and 96 may divide 96 but not 146. As a result, it cannot be GCD. So, we can avoid this iteration by including a check before the loop, as-
int small = Math.min(number1, number2);
int large = Math.max(number1, number2)
if(large % small == 0)
result = small;
else
small /= 2;
//Loop continues
This optimization saves some computational time, but the Asymptotic time complexity remains O(n) because the loop must be traversed at most (n/2) times.
So, in order to optimize this, we can use the same division method that we used in school to calculate the GCD or HCF of two values.
Approach - First, we determine the lowest integer between 2 and use it as the divisor. And the greatest input number will be our dividend. Then we divide it till the remainder equals zero. Until the remainder is greater than zero. The remainder will then become a divisor, and the current divisor will become a dividend. And the updation of divisor and dividend must be repeated till the remaining equals zero. This method is also known as Euclid's Algorithm.
Let's look at an example to better grasp how things function. Given Two input numbers: A = 176 & B = 96. Consider the image below for clarification.
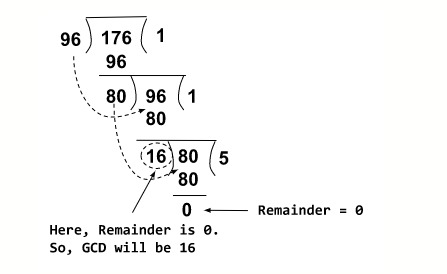
In the figure above, we divide the integer till we receive a remainder of 0. When the remainder equals zero, the current divisor is the GCD.
Algorithm for the above Approach- We can divide these processes into two algorithms. Specifically, recursive and iterative algorithms. Recursive Algorithm - We can see from the steps below that it is developing a recursive pattern. On each next step, we are finding the remainder and updating the divisor and dividend. So we can use recursion to solve this.
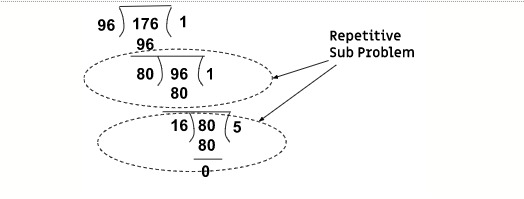
- Define the function that takes divisor and dividend as arguments.
- Check to see if the divisor can divide the dividend entirely. Return the divisor if yes.
- Call the function recursively by supplying the divisor as the remainder of the divisor and dividend. As well as dividend as the current divisor.
Java program for the above algorithm is -
import java.util.Scanner;
class InterviewBit {
//Recursive Method
private static int gcd(int divisor, int dividend){
//Calculating Remainder
int rem = dividend % divisor;
//Base Case if rem is equal to 0 then divisor is gcd.
if(rem == 0)
return divisor;
//Recursively finding the gcd.
return gcd(rem, divisor);
}
public static void main(String args[]) {
//Scanner class helps accepting user inputs. So accepting
//and storing in variables.
Scanner sc = new Scanner(System.in);
int number1 = sc.nextInt();
int number2 = sc.nextInt();
//Calculating dividend and divisor.
int dividend = Math.max(number1, number2);
int divisor = Math.min(number1, number2);
//Calling Method for finding the gcd.
int result = gcd(divisor, dividend);
//Printing the result.
System.out.println("GCD of "+number1+" and "+number2+" is = "+result);
}
}
Run this code on InterviewBit
Input - 96 176
Output - GCD of 96 and 176 = 16.
Iterative Algorithm - We may change the recursive algorithm into the iterative algorithm by evaluating it. We can loop till the remaining is not equal to 0. As a result, the Algorithm will be -
- The dividend and divisor should be calculated.
- Calculating the Remainder.
- If the remainder is zero, output the divisor as the gcd and go to step 5.
- Otherwise, update the dividend as a divisor and the divisor as a remainder before proceeding to step 2.
- Exit.
Java program for the above algorithm is -
import java.util.Scanner;
class InterviewBit {
public static void main(String args[]) {
//Scanner class helps accepting user inputs. So accepting
//and storing in variables.
Scanner sc = new Scanner(System.in);
int number1 = sc.nextInt();
int number2 = sc.nextInt();
//Calculating dividend and divisor.
int dividend = Math.max(number1, number2);
int divisor = Math.min(number1, number2);
//Calculating the remainder.
int rem = dividend % divisor;
//Loop that calculates the remainder and updates the divisor and dividend.
while(rem != 0){
dividend = divisor;
divisor = rem;
rem = dividend % divisor;
}
//Printing the result.
System.out.println("GCD of "+number1+" and "+number2+" is = "+divisor);
}
}
Run this code on InterviewBit
Input - 96 176
Output - GCD of 96 and 176 = 16.
Analysis of the Approach
We update the value based on the remainder in both the recursive and iterative algorithms. So, if we study the method, the precise number of steps that it will take is - O(log rem (min(divisor, dividend)). However, it is most often known as O(log n). Despite the fact that the real-time is less than O(log n). Because of the recursive call stack, the recursive algorithm requires O(log n) extra space. And the iterative approach requires just a constant O(1) space.
Conclusion
The mathematical tool GCD (Greatest Common Divisor) describes the number that may divide both numbers. We've seen the Java code used for implementing the algorithm. We also have understood the algorithm's analysis to determine how optimum the algorithm is. The best approach for determining the GCD of two integers (Euclid's Algorithm) really aids in reducing complexity during competitive programming.


Comments (0)