Trees

A Tree is a non linear data structure. Unlike the data structures that we've learned so far like - Linked Lists, Stacks, Queues, etc. In this type of data structure, one element can be linked to more than one element.

Tree data structure, just like the other data structures we've learned so far, is an example of abstract data type.

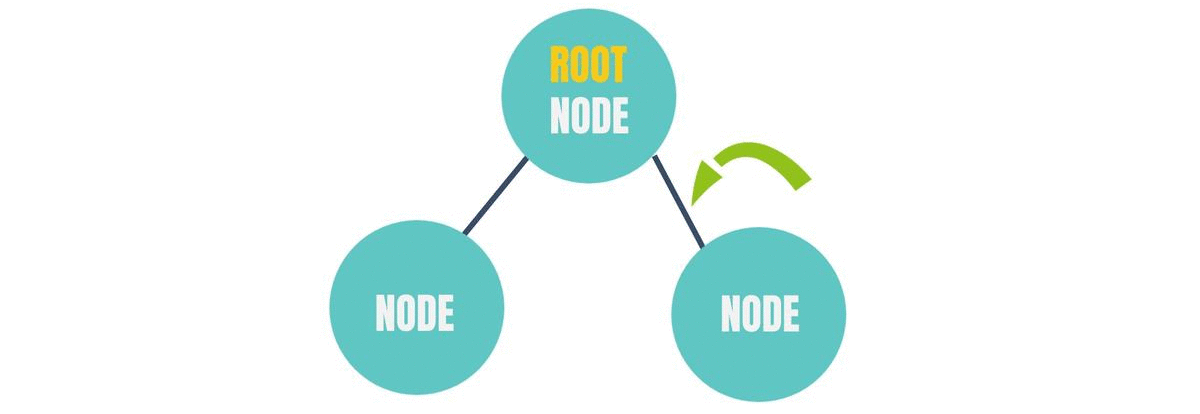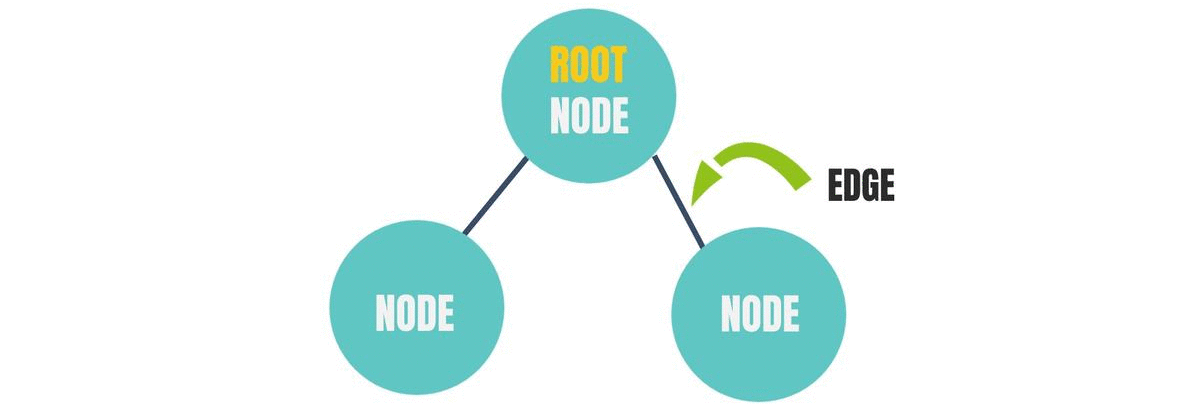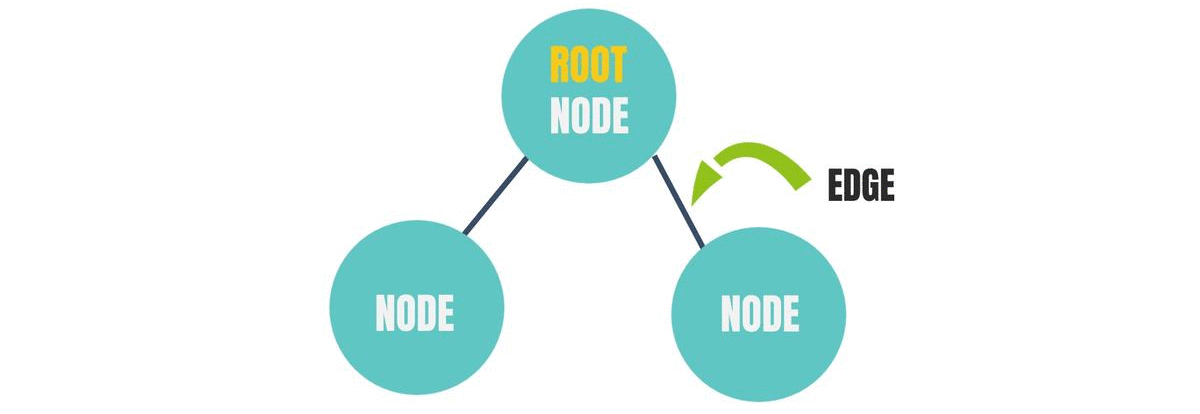
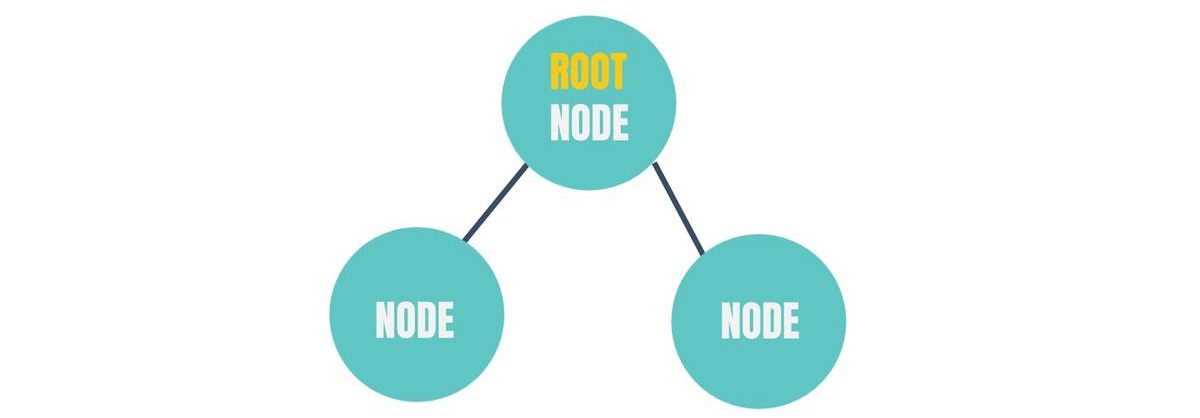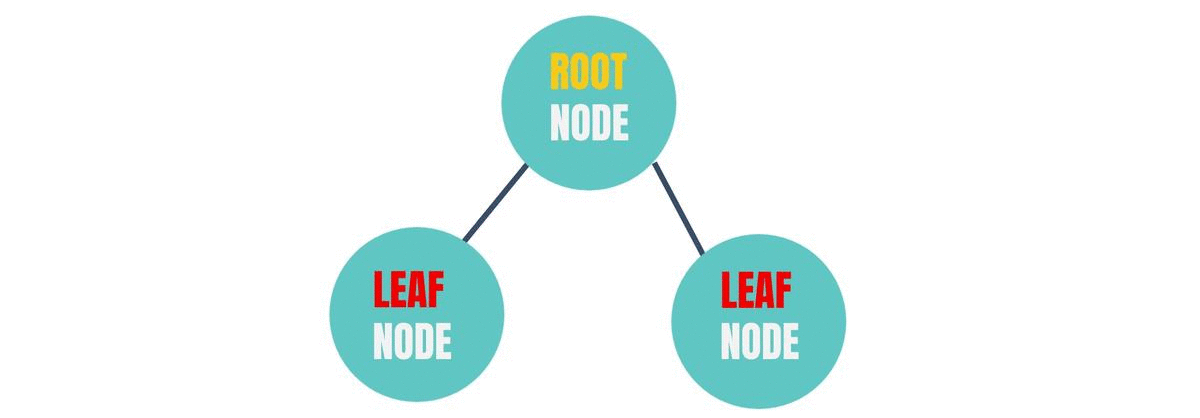
The tree data structure looks sort of like this - 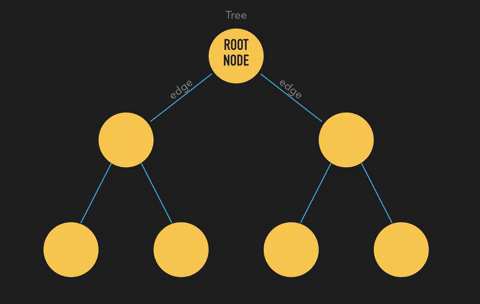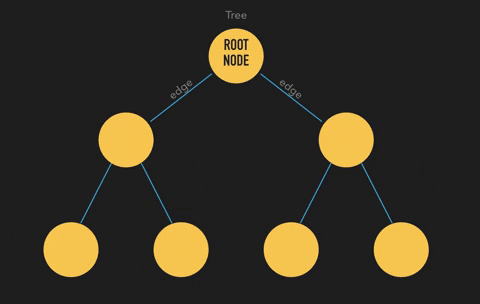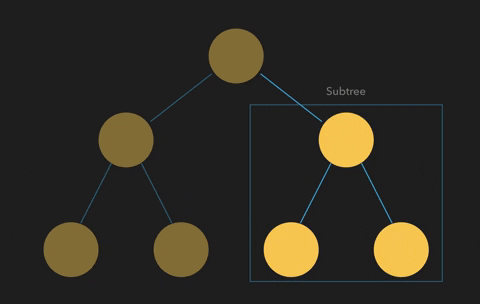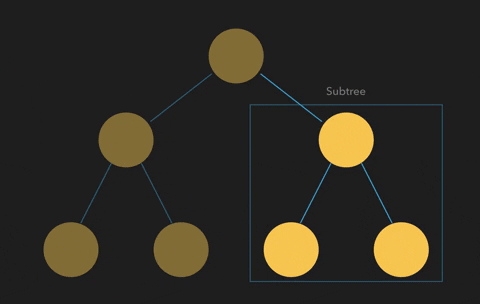Just like a linked list, each of those circles or units that you can see in the above figure is called a "Node".

Basic Definitions

To be able to understand the Tree data structure perfectly, you'll need to pay a lot of attention towards the terminologies used in it.

Some of the basic terms used in it are - Root Node

In the above figure, the topmost node that you can see is called the "Root Node". The name is pretty much self explanatory, doesn't it look like the origin point of roots of a plant? Edge

The lines that are connecting each pair of nodes in the above diagram is called an "Edge".

Leaf Node

The node which is not connected to any other node below its level is called a "Leaf Node".

🤩 Our Amazing Sponsors 👇

View Website

DigitalOcean offers a simple and reliable cloud hosting solution that enables developers to get their website or application up and running quickly.

View Website

Laravel News keeps you up to date with everything Laravel. Everything from framework news to new community packages, Laravel tutorials, and more.

View Website

A Laravel Starter Kit that includes Authentication, User Dashboard, Edit Profile, and a set of UI Components. Learn more about the DevDojo sponsorship program and see your logo here to get your brand in front of thousands of developers.

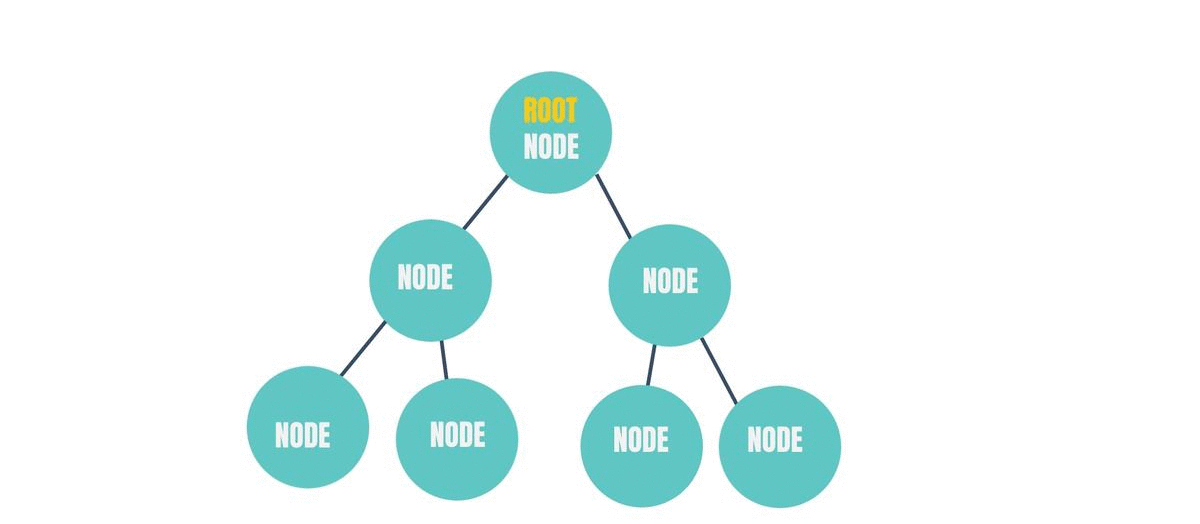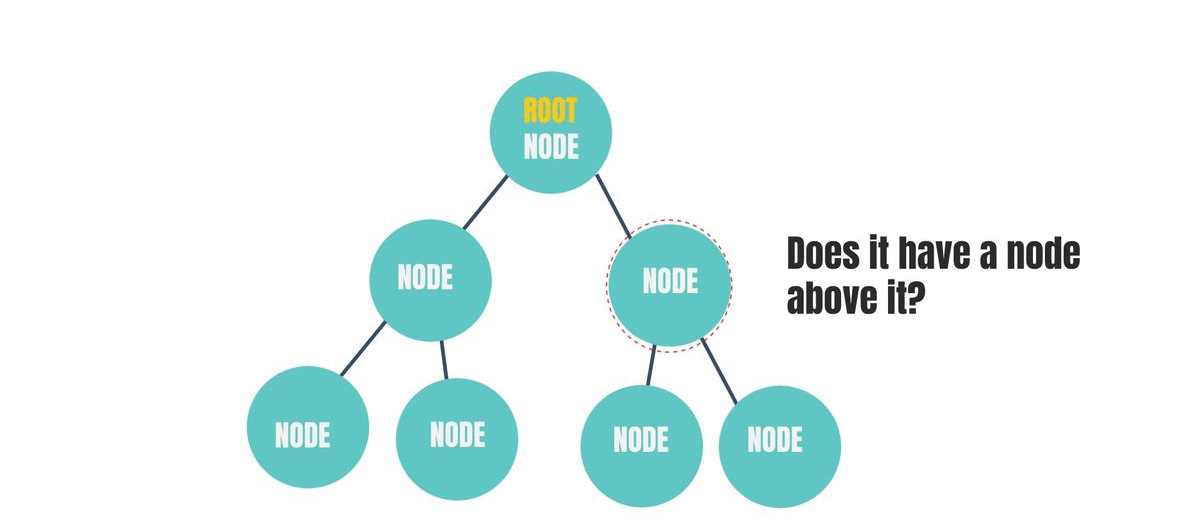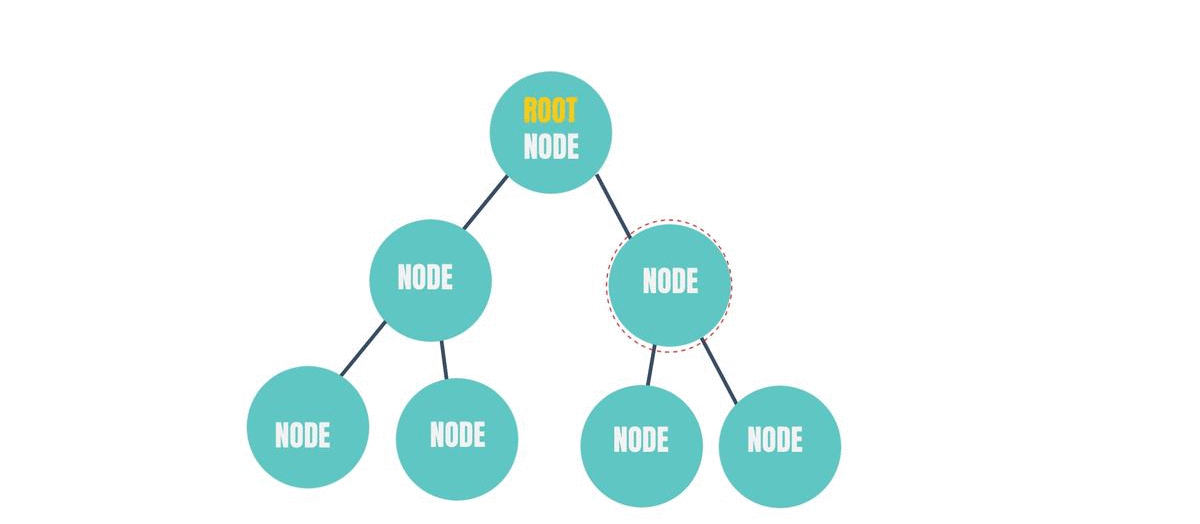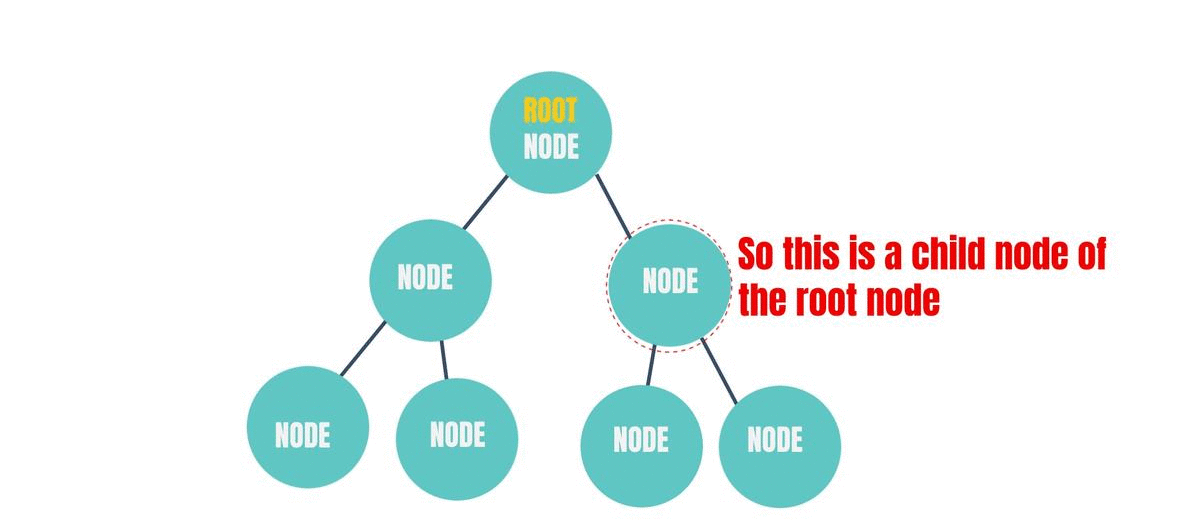
Child Node

Choose a random node in the above diagram. Does it have a Node above it? If it does, then it is a "Child Node" of the Node above it. If it doesn't then it is the root node. A root node can never be a child node. If we add a node above the root node, then it no longer remains the root node.

Parent Node

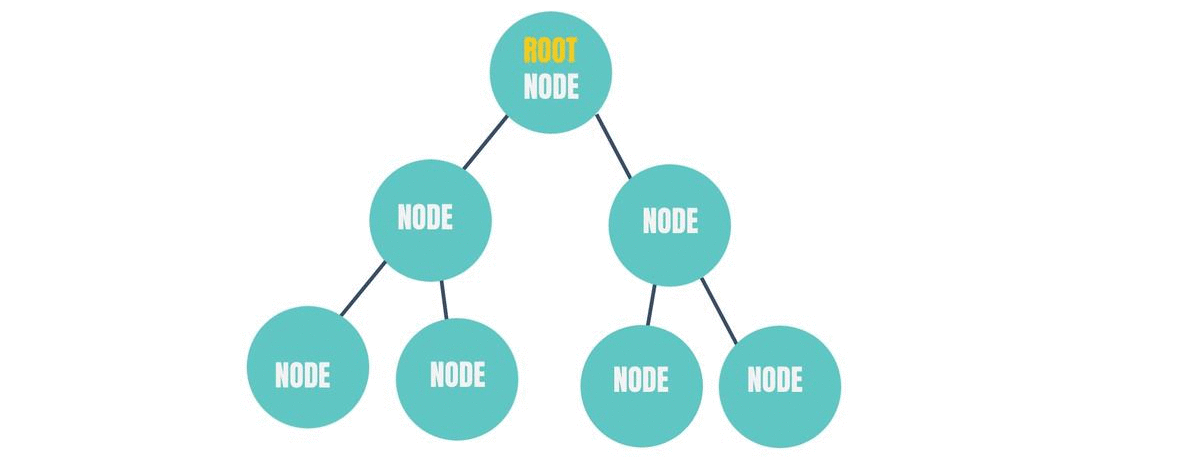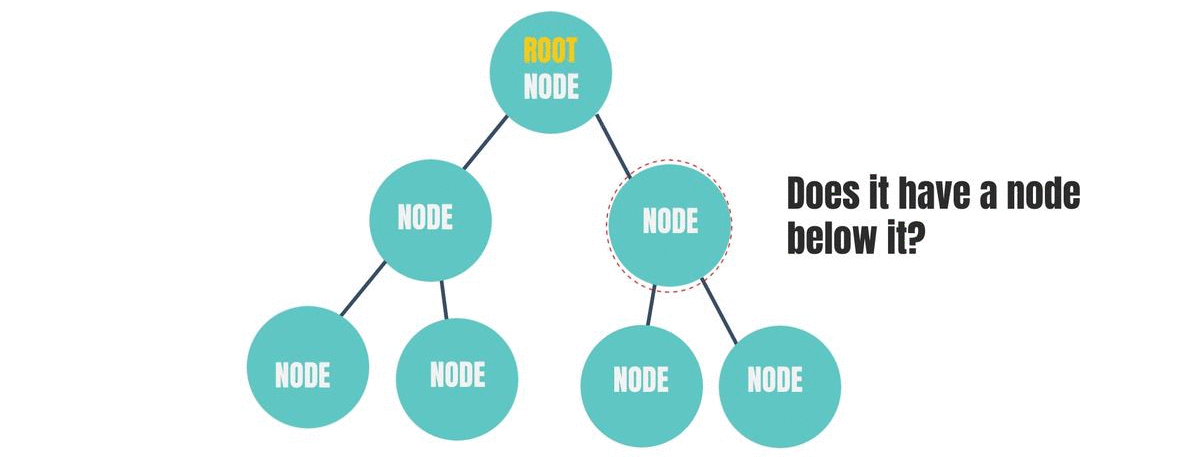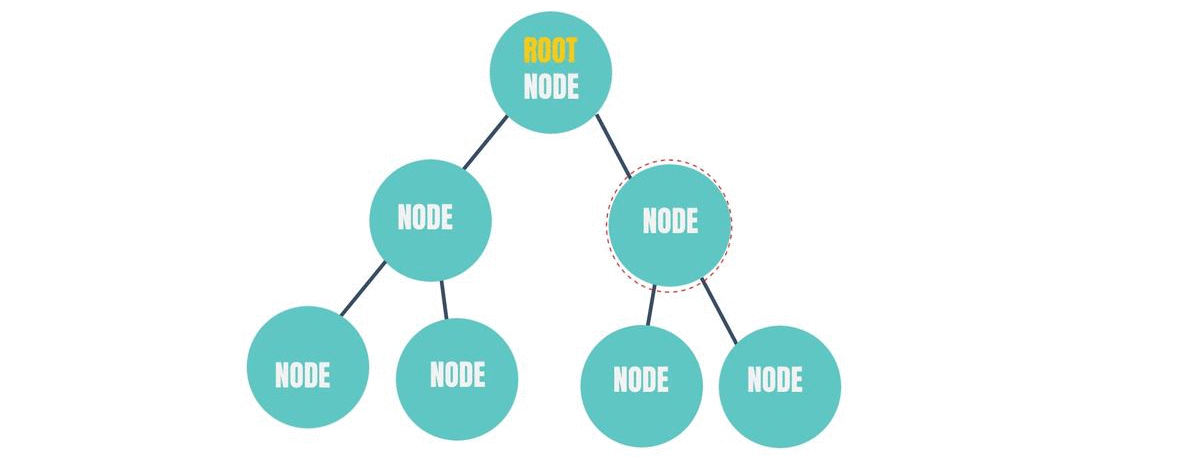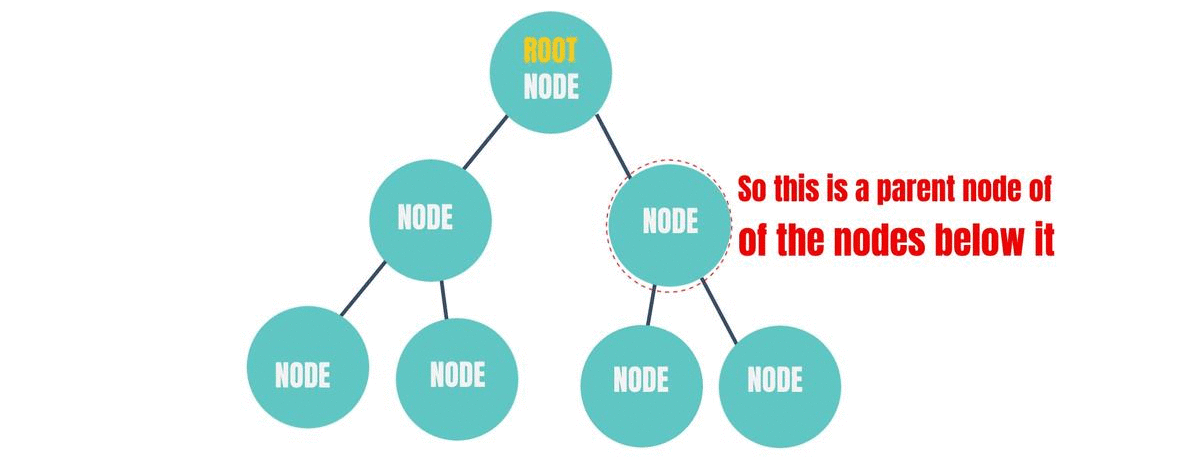
Again, choose a random node in the above diagram. Does it have a Node below it? If it does, then it is a "Parent Node" for the node(s) below itself. If it doesn't have anything below it, then it is a leaf node. A leaf node can never be a Parent Node. If you add a node below a leaf node, then it would no longer be a leaf node.

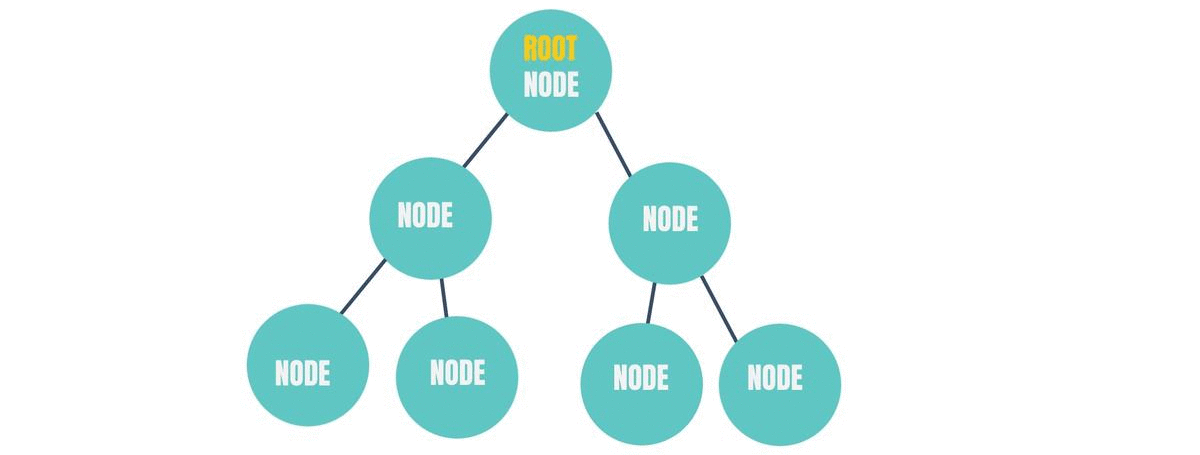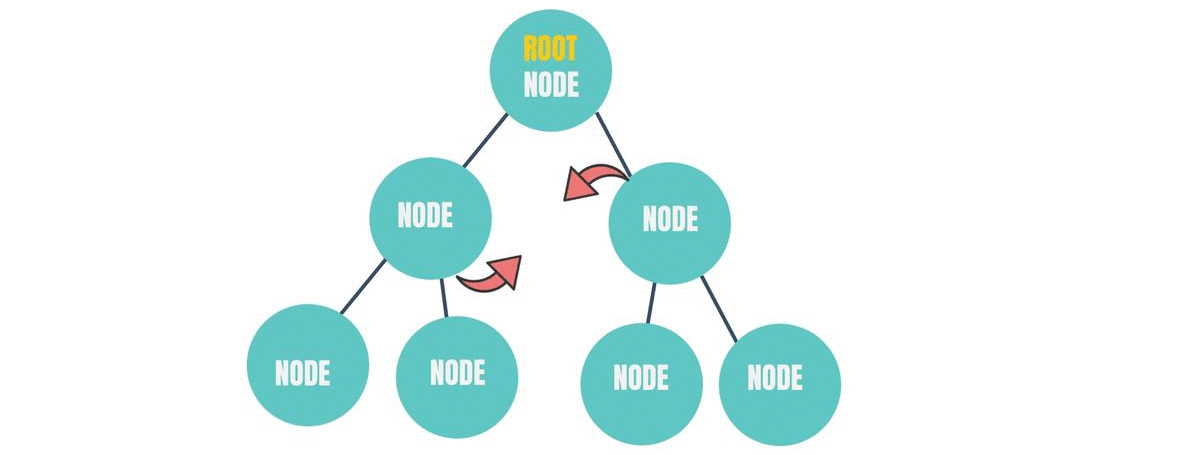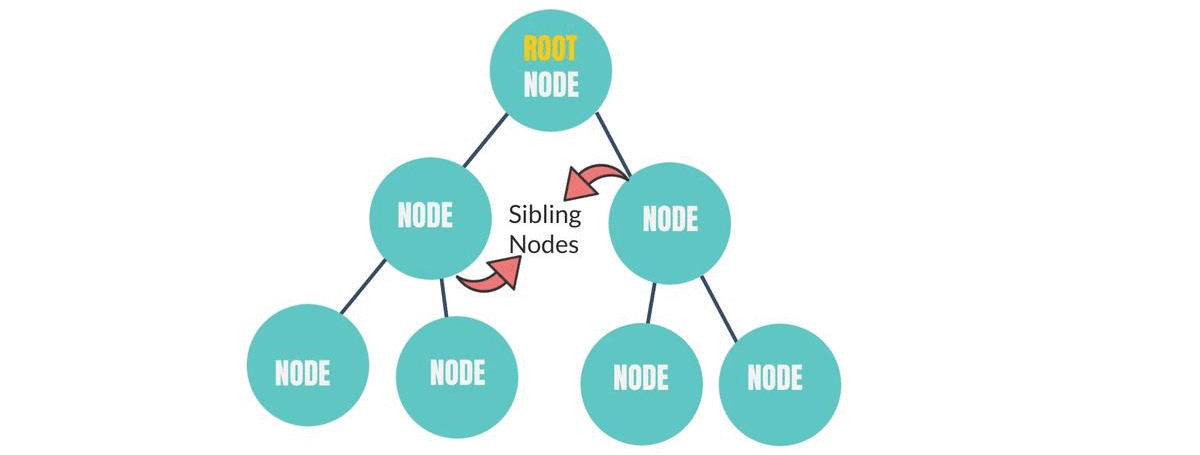
Sibling Nodes

The nodes that have the same parent node are called "Sibling Nodes".

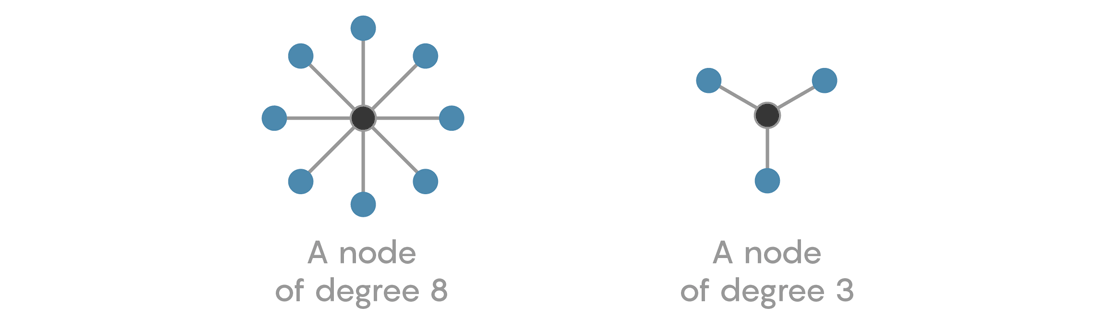
Degree of a Node

The number of Nodes a Node is connected to is called "Degree" of that Node.

Types of Trees

Now that we know the basic terminologies of a Tree, let's talk about the types of trees you will come across in Data Structures.

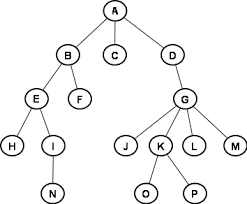
1.Normal Tree

This type of tree is free of all constraints. The word "Constraints" here mean, how we insert and delete the nodes based on the values of the nodes of the tree, how we adjust the arrangements nodes of the tree after insertion or deletion, how many children a node can have in the tree and so on.

2.Binary tree

In this type of tree, a node can not have more than 2 child nodes.

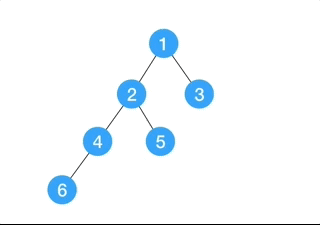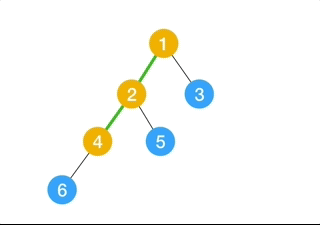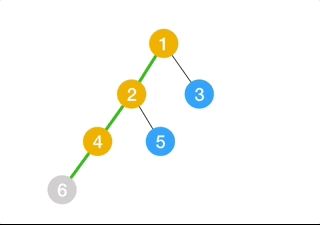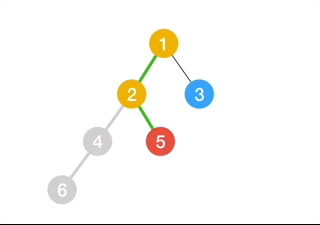
3.Binary Search Tree

This is also a binary tree but, here the left child node should have a smaller value than the parent node value and the right child node should have a value greater than the parent node.

4.AVL Tree

It is a self balancing tree. It is also a type of Binary tree. We'll learn about the balance of a tree as we go deeper into this topic. There are many more trees in Data Structures, but the above are the most common ones.

This is it

I hope you liked this article. Check out my other articles here.

Happy Learning!