The process of insertion in a Heap is not as easy as it is in a normal binary tree. In a normal binary tree, you can simply insert an element at the first empty spot you find. But, in a heap(which is a complete binary tree following a specific order of placing the elements inside it), it gets much more complicated than simple insertion in the case of a normal binary tree as we have to maintain the complete binary tree structure as well as fill up the tree in order.
The Algorithm
A heap contains two very important features that make it different from a normal binary tree -
- It is a Complete Tree.
- It is Ordered Level-wise(based on the kind of heap we're trying to make).
So, Our first step for the algorithm would be, to insert the new element into the heap such that its property of being "Complete" is maintained. In other words, you can insert the new element in the leftmost empty spot in the heap such that none of the levels above that level has any empty spot.
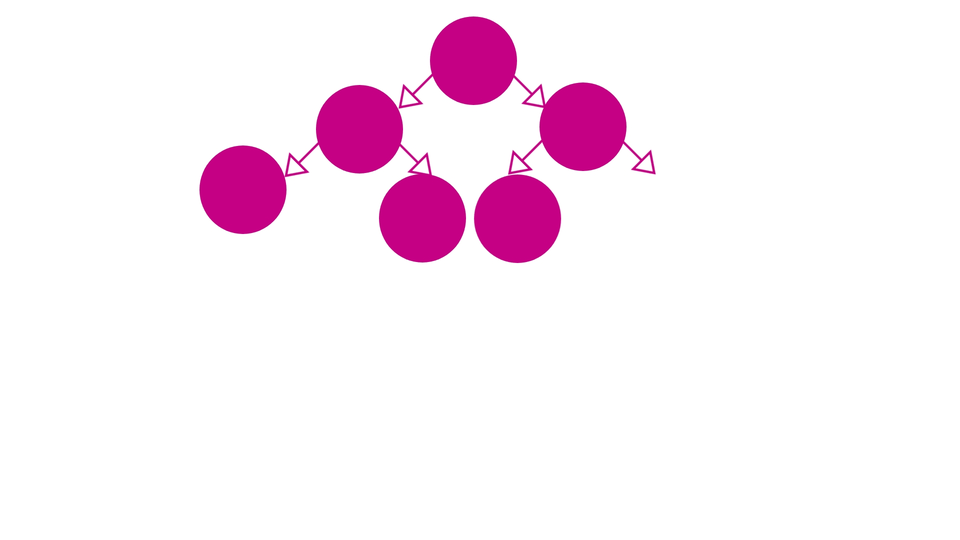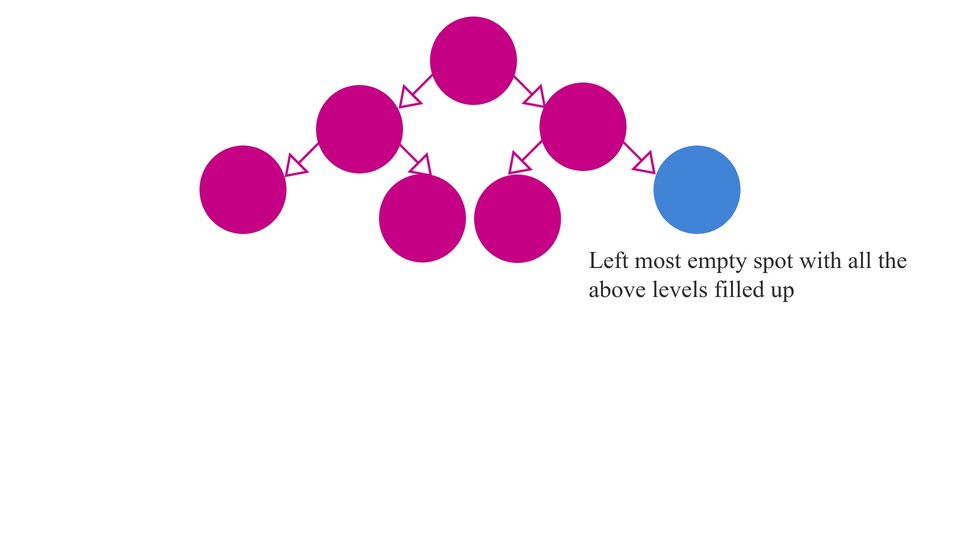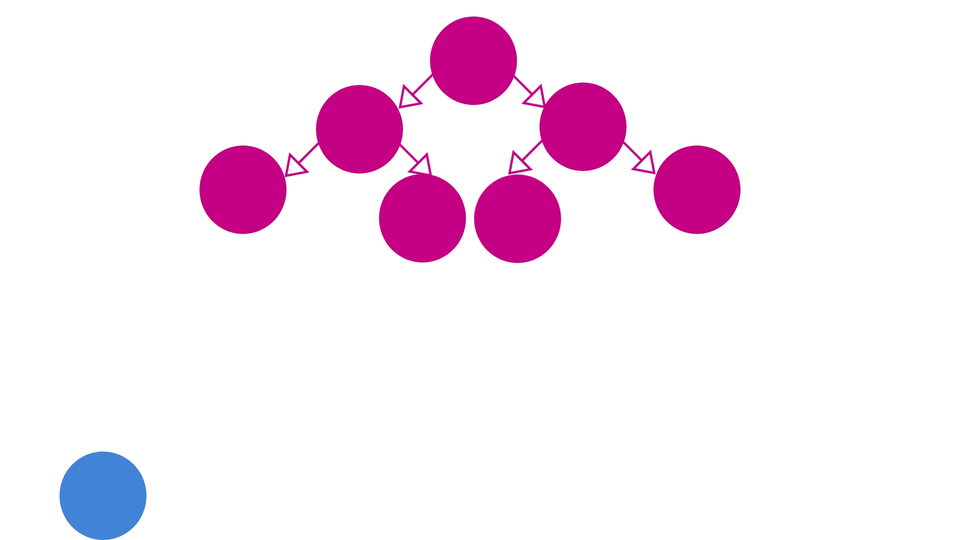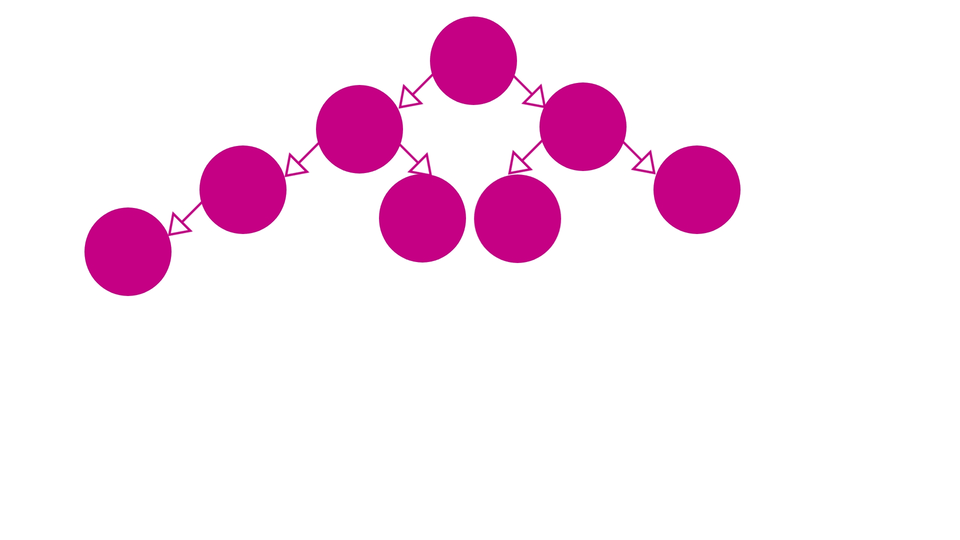
Our second step is - to swap elements among the levels of the heap, so as to maintain the order of the elements. For example, if we're trying to insert a new element in our min-heap, we'll first try to insert it in the next empty spot while maintaining the completeness of the heap and then we swap it until the order is restored.
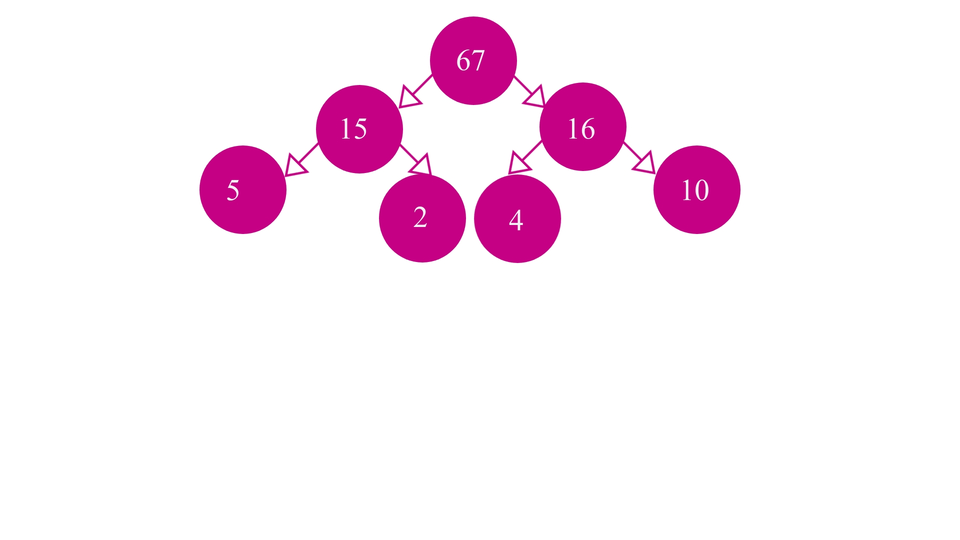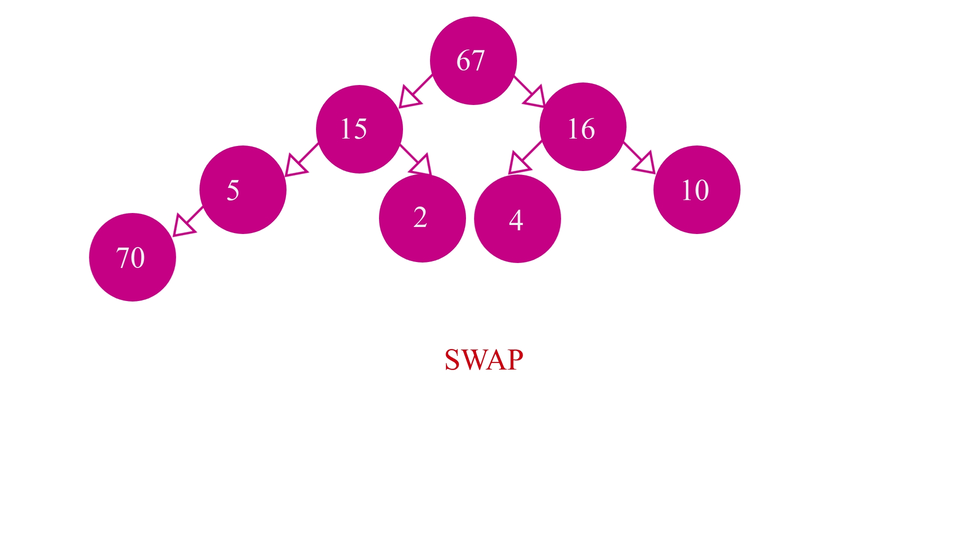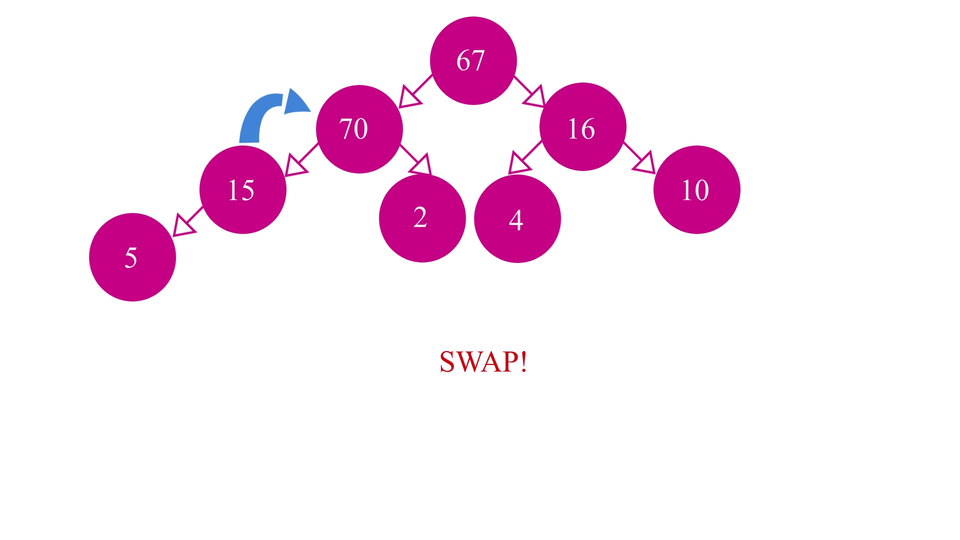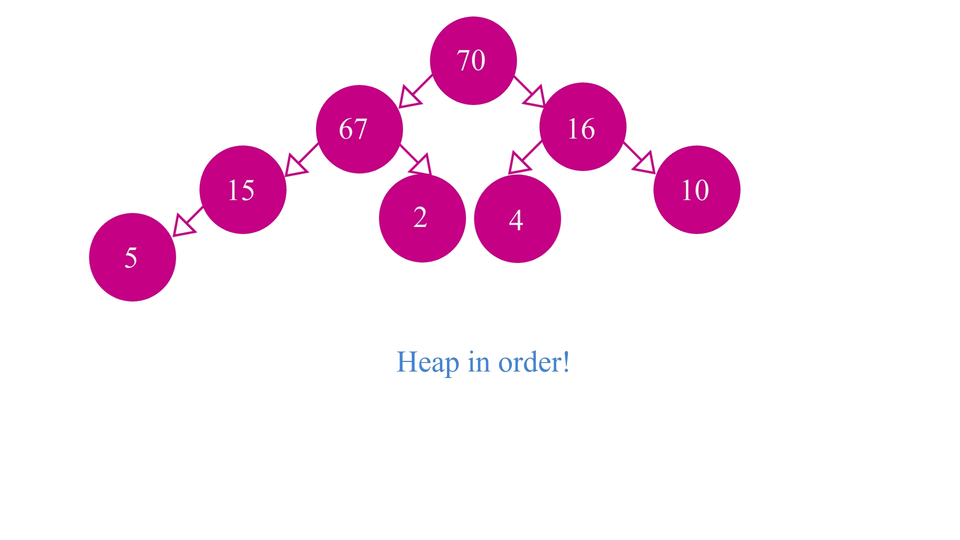
Now, we're not going to do all these processes on an actual heap as that would be time taking and complicated. Instead, we are going to use array representation of heaps.
We're going to make use of the formulae that are used to calculate the index value of the parent node, left child node, and right child node of an element in the array using its index value -
- Left child node index value = 2*i+1
- Right child node index value = 2*i+2
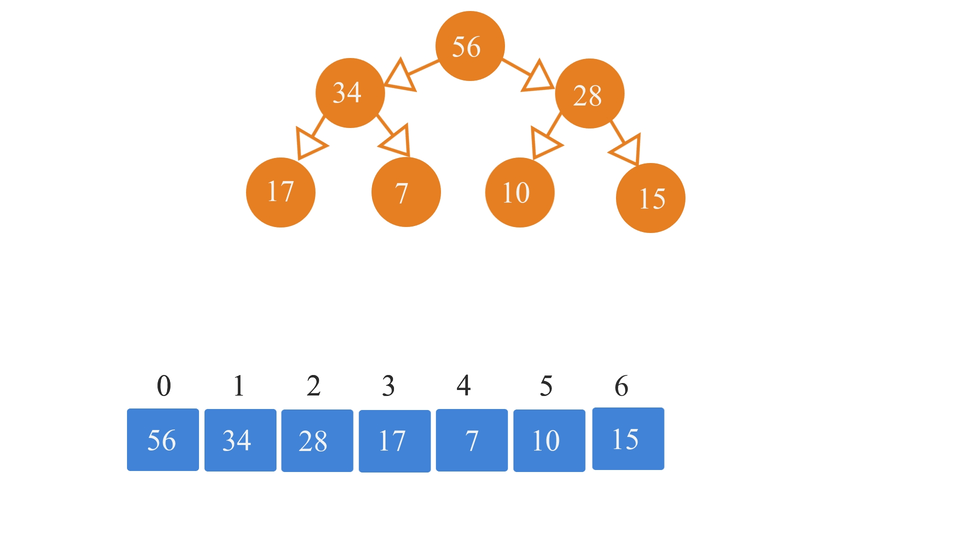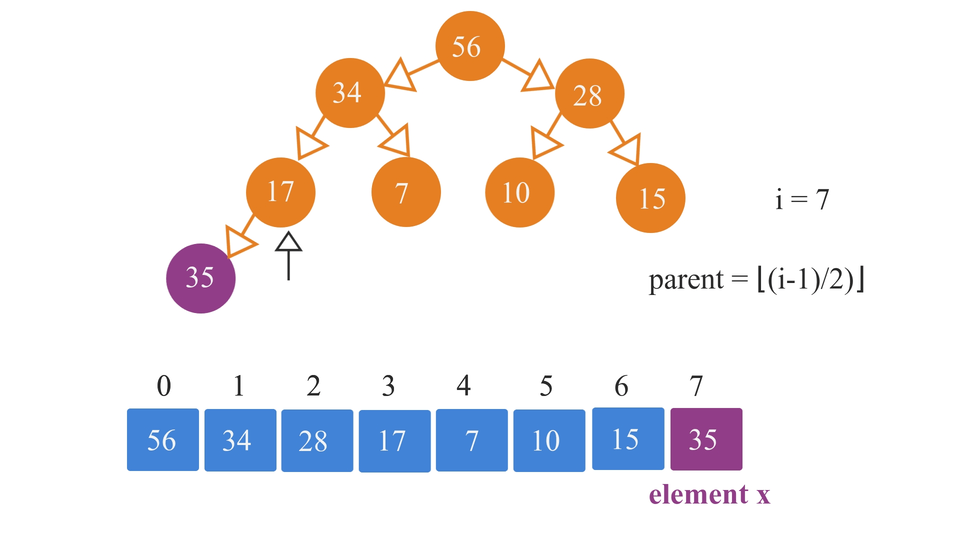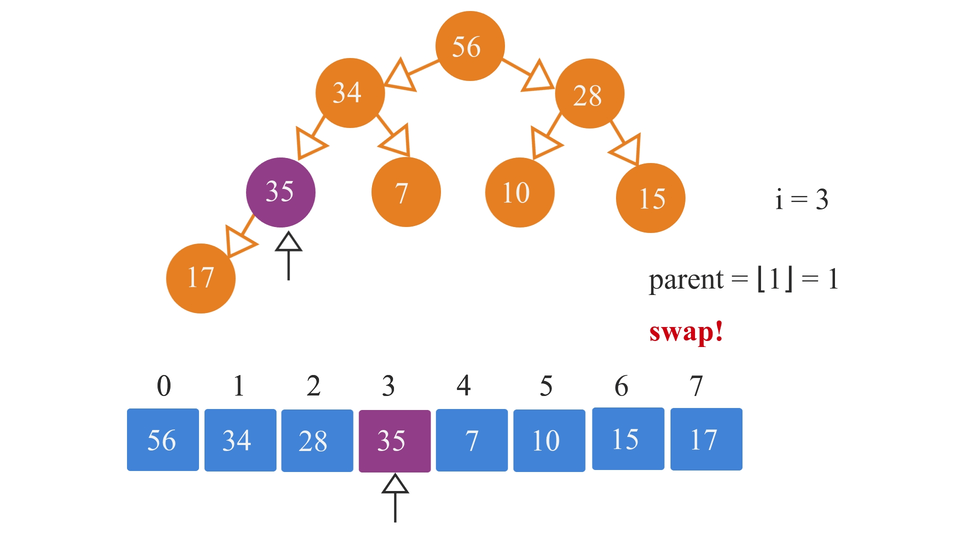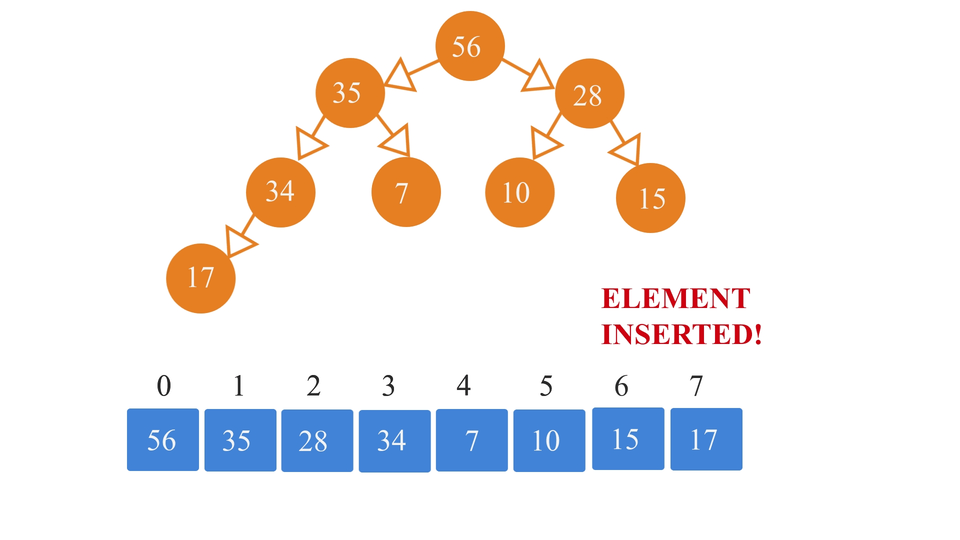
- Parent node index value = ⌊(i-1)/2)⌋
Here "i" is the element whose right/left child node or parent node is being computed. We start with the root node. The root node is filled in at index 0 of the array.
If you already have a heap and you want to convert it into an array, you can follow this simple algorithm for it -
- start with the root node.
- Insert the root node at index 0.
- Compute, left and right child's index value using the formulae and insert the left and right child node values into the array at the computed indices.
- Move to the next filled-up index position in the array(say i'th element in the array).
- Again, calculate the i'th element's left and right child index positions in the array and insert their value in the array. Basically, you have to repeat the steps 3-4 again and again until you fill up the array.
So, the process looks something like this -
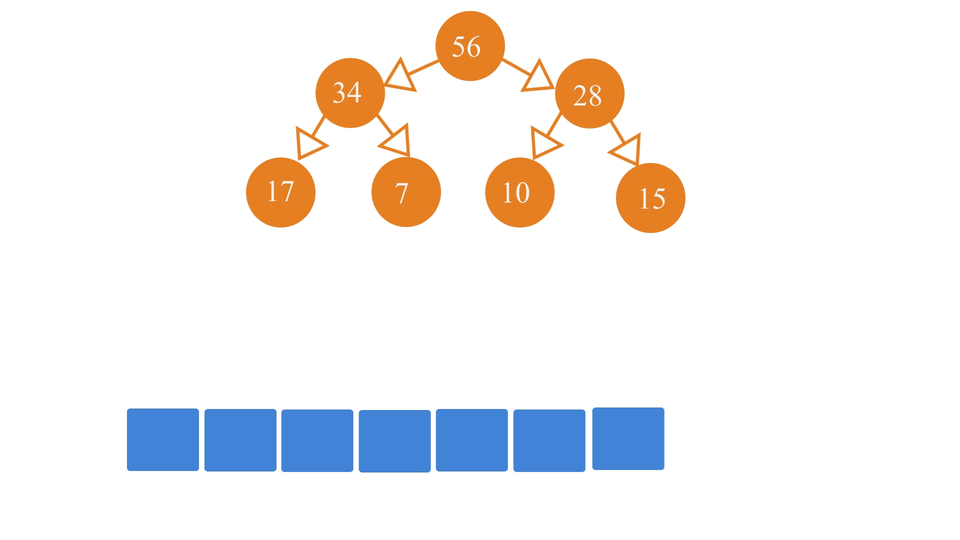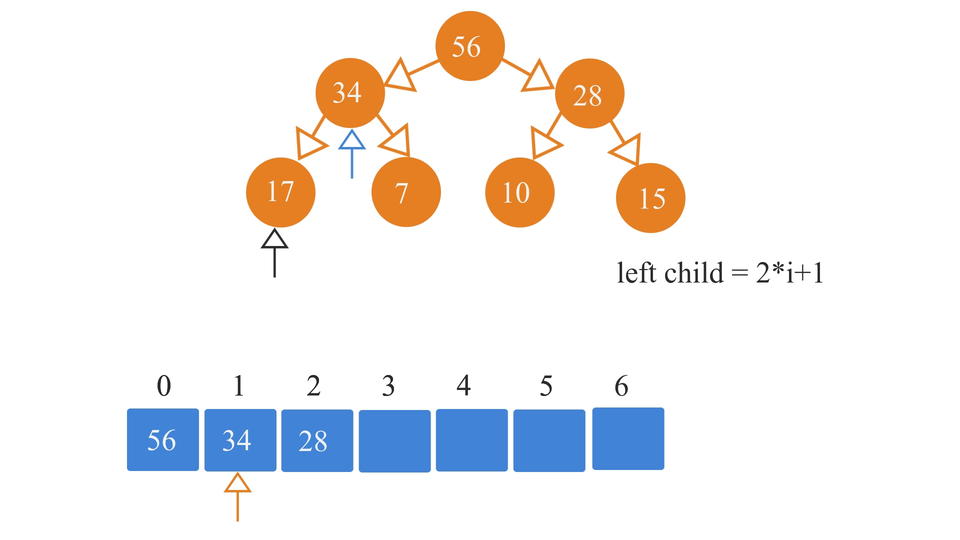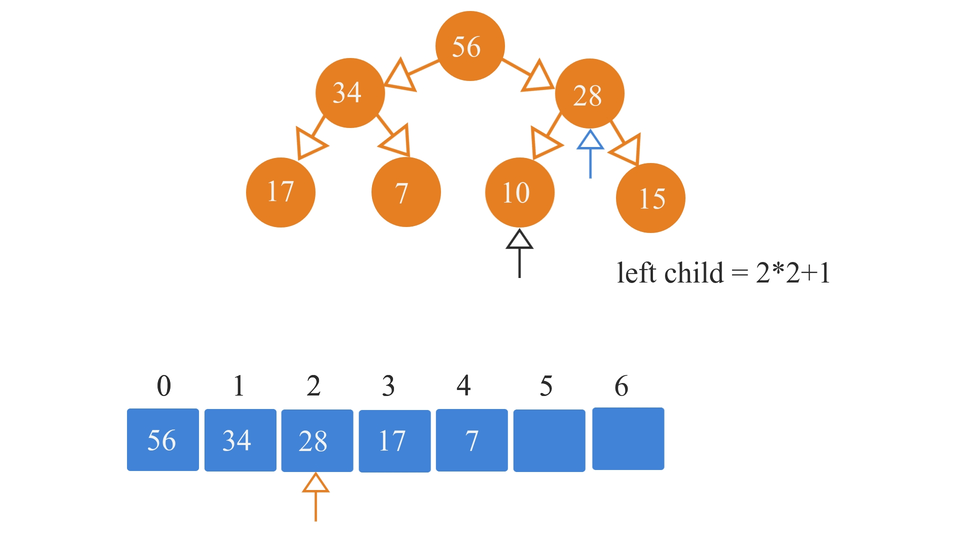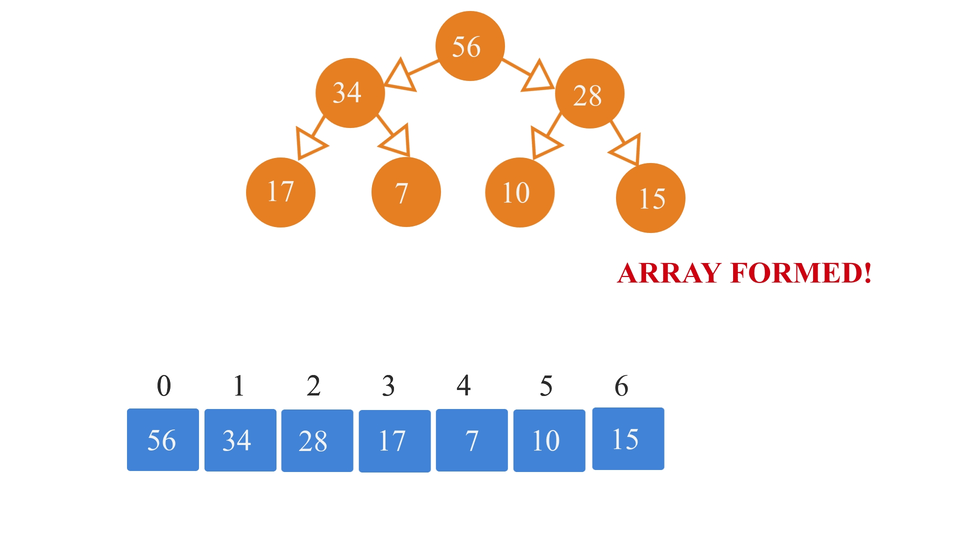
If in case you want to insert an element in a heap(in its array form), you just have to insert that element in the next empty spot and then just swap it until the order of the elements of the heap is restored. For that, you can follow the following algorithm -
 View Website
View Website
 View Website
View Website
 View Website
View Website
- Let's say we have an array "arr" with pre-inserted elements of the heap.
- We're planning to insert element "x" into the heap(in it's array form).
- INSERT: First, we just simply insert it at the end of the array(temporarily). Inserting an element at the end of the array means it has been inserted at the next empty spot of the heap.
- SWAP: Then we compare this element "x" with its parent. If suppose, we're trying to insert in a min heap, and x is smaller than its parent, then we swap the two. Otherwise we just let it be as it is. Vice versa for a max heap.
And that's it!
The Code
Code for converting heap into an array
#include <stdio.h>
#include <math.h>
int main(){
int n;
printf("Enter total number of elements in the array: ");
scanf(" %d", &n);
int arr[n], i=0;
while(i < floor((n-1)/2)){
if(i == 0){
//this is the root node;
printf("Enter value for root node: ");
scanf("%d", &arr[i]);
printf("Enter value for left child node of root: ");
scanf(" %d", &arr[2*i+1]);
printf("Enter value for right child node of root: ");
scanf(" %d", &arr[2*i+2]);
}else{
printf("\tFOR NODE NO. %d: \n", i);
printf("Enter value for left child node: ");
scanf(" %d", &arr[2*i+1]);
printf("Enter value for right child node: ");
scanf(" %d", &arr[2*i+2]);
}
i++;
}
printf("THE ARRAY IS: \n");
for(int j=0; j<n; j++){
printf("%d ", arr[j]);
}
}
We'll need to include math.h header file in our program to be able to work with floor division operation in C.
Code for insertion into a heap
#include <stdio.h>
#include <math.h>
#include <stdbool.h>
#define MAX 20
int main(){
int arr[MAX], n;
printf("Enter number of elements in the heap: ");
scanf(" %d", &n);
for(int j=0; j<n; j++){
printf("Enter element: ");
scanf(" %d", &arr[j]);
}
n--;
//arr is already having heap elements
//we'll insert an element into the heap(arr).
while(true){
int x;
printf("Enter the element you want to insert: ");
scanf(" %d", &x);
printf("Inserting %d...\n", x);
n++;
int i = n;
//insert the element at the end of the array;
arr[i] = x;
int parent_idx = floor((i-1)/2);
while(arr[parent_idx] < arr[i]){
//swap the two
int temp = arr[parent_idx];
arr[parent_idx] = arr[i];
arr[i] = temp;
i = parent_idx;
parent_idx = floor((i-1)/2);
}
printf("Heap array is updated to: ");
for(int j=0; j<n+1; j++){
printf("%d ", arr[j]);
}printf("\n");
int ch;
printf("Do you want to continue insertion?(1 for continue, 0 for exit): ");
scanf("%d", &ch);
if(ch==0){
break;
}
}
}
Note that here I've initially taken array element input straight from the user. These elements are the elements of the heap in array format(for situation when you already have a heap of n number of elements and you're just trying to add an extra element in the heap). You can replace that part with the first code snippet which is for the purpose of converting a heap into an array, if you already have a heap and you want to convert it into array and work with it accordingly. If you don't have a heap beforehand, you can just enter 0 when "number of elements in the heap" is asked.
Conclusion
This is all about insertion of elements in a heap in array format. I hope you got a good idea about the procedure of how it can be implemented through this article. You can read more such interesting articles on Data Structures and Algorithm in C here.
Thanks for reading!☃


Comments (0)