In this post I'm gonna be talking about deletion of a node in Binary Search Tree.
There can be three scenarios for deletion of a node in a Binary Search Tree.
Let's first discuss the three scenarios.
The three situations of deletion
1. Node to be deleted is a leaf node
It has the easiest deletion procedure. When you want to delete a leaf node, deletion happens like in a normal linked list as the node doesn't have any child node to care of. You just simply have to point child node of the targeted node's parent node to null and then free the space allocated to the targeted node.
2. Node to be deleted has one child node
It's a little more complex than the previous method. In this case, there is one child node to take care of and we cant simply delete the targeted node. So, we swap the targeted node with its child node, swapping continues till we reach a leaf node, then finally the leaf node(containing the targeted node's value after some swaps) is deleted.
3. Node to be deleted has two children
It has the most complex deletion method. In this situation, we'll have to swap the targeted node with its immediate "in-order successor" (the element that succeeds the targeted element in in-order traversal of the tree) until it reaches a leaf node. Finally, the leaf node is deleted.
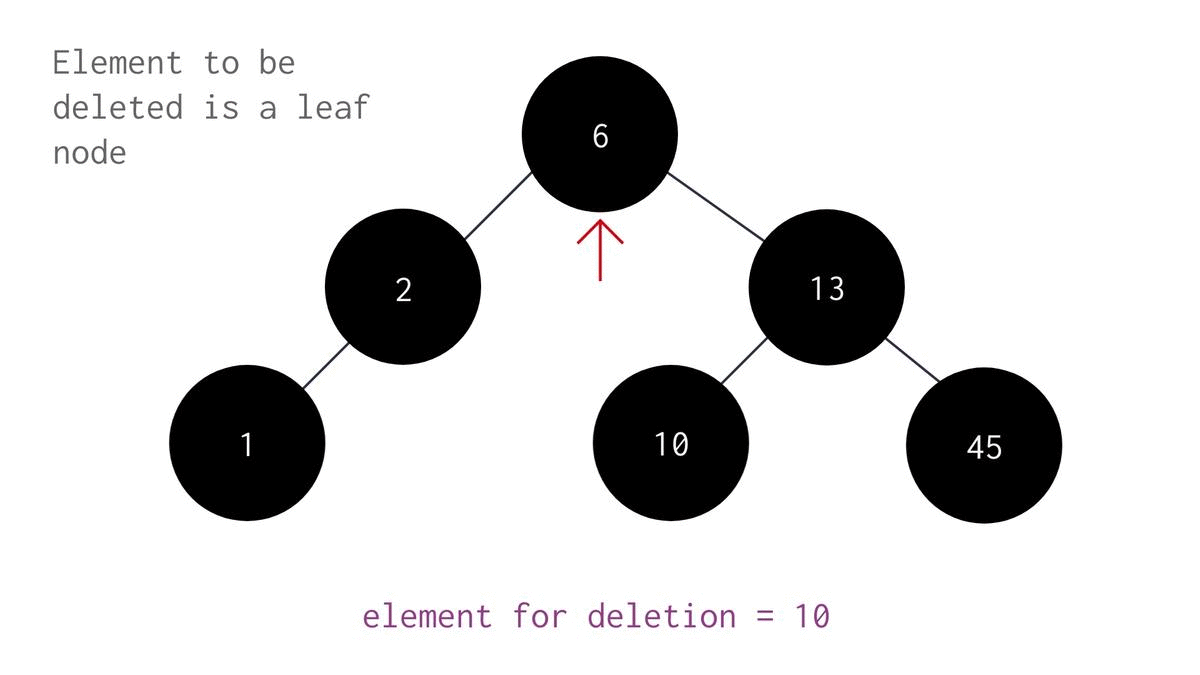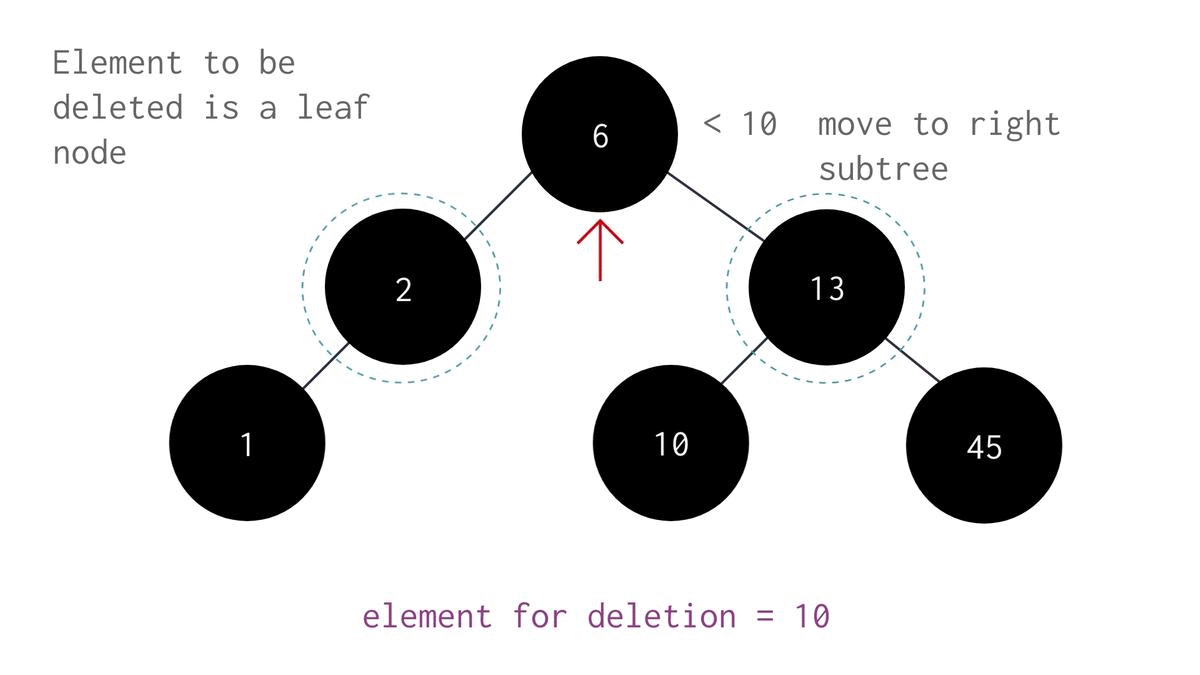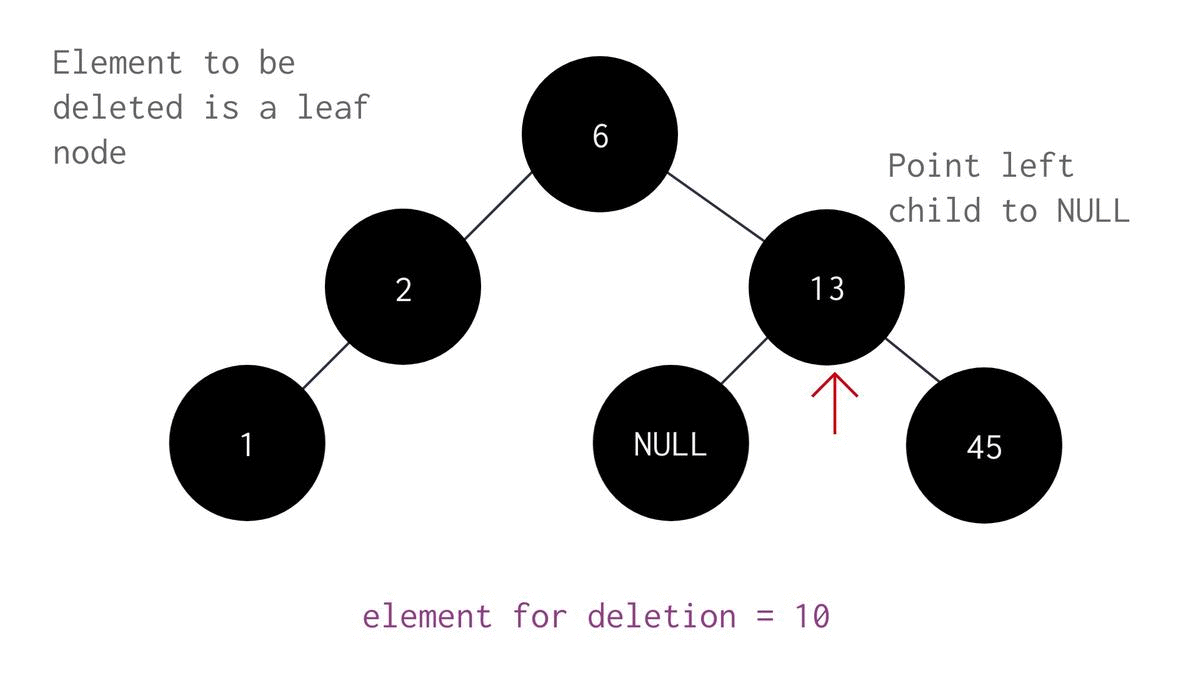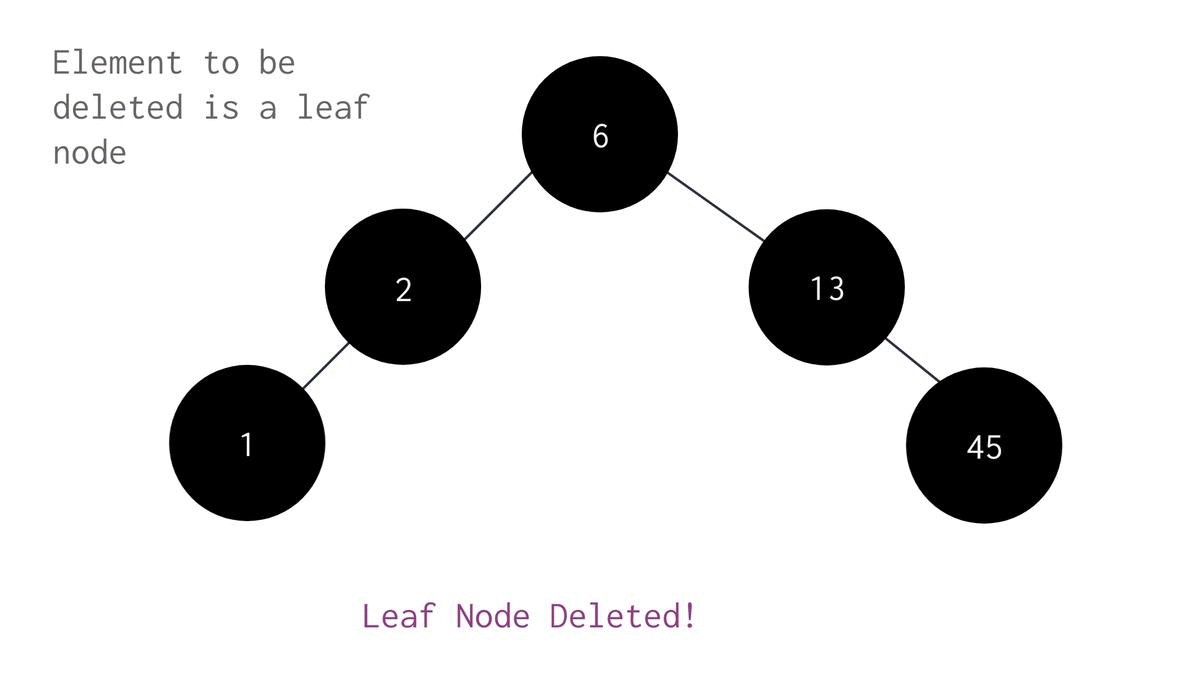
Deletion of leaf node
If you want to delete a leaf node, all you have to do is move the pointer to the parent node of the targeted node and then point its child node to null.
To make the pointer point at the targeted value's parent node, we'll have to search the targeted node.
To search for an element in a binary search tree, you have to compare the targeted value with the elements of the tree starting from its root as the parent node. If the value is greater than the parent node, move to the right child otherwise move to the left child and repeat the above steps until the targeted node is reached.
View Website
View Website
View Website
You can check out my post here on how to perform search in a binary search tree.
Algorithm:
- Check if root is empty or not. If so, print "Empty Tree". Else do the following:
- If root value is greater than user entered value "val", check if its child node is val or not. If it is, then point its left child to NULL. If not, then traverse further into the left subtree.
- If root value is less than "val", check if its child node is val or not again. If it is, then point its right child to NULL. Else, traverse further into the right subtree.
- If root node is the target node as well as a leaf node, set root to NULL.
Following is the C code for deletion of a leaf node:
void deleteLeafNode(int val, NODE *root){
if(root == NULL){
printf("Empty Tree!\n");
}else{
if(root->data > val){
//traverse in left subtree
if(root->left->data == val){
//parent node for target found
root->left = NULL;
}else{
deleteLeafNode(val, root->left);
}
}
else if(root->data < val){
//traverse in right subtree
if(root->right->data == val){
//parent node for target found
root->right = NULL;
}else{
deleteLeafNode(val, root->right);
}
}
else{
//root node is the target and root is leaf node.
root = NULL;
}
}
}
Note that this code would only work for deletion of leaf nodes. It will not work for nodes that have a single or both child nodes.
This is just an example to give you an idea about how you can perform deletion in a binary tree.
A general code for deletion for all three cases
Here, we're gonna derive a general code that will work for deletion of nodes with any number of child nodes(0, 1, 2). As we discussed earlier, if a node has 1 or 2 child nodes, we have to swap the target node with its "in-order successor" until the target node becomes a leaf node. This is how we do it -
- Find the targeted value in the Tree.
- Find the in-order successor of the targeted node in the tree.
- Swap the targeted node and and the in-order successor.
- If targeted node becomes leaf node, set the targeted node value to NULL. If leaf node state not reached, Repeat all the above steps again.
To find the in-order successor of the target node, we'll make a function called "RightMin" which will fetch the left-most node(or smallest node) in the right subtree of a node (which basically means the in-order successor). Algorithm for RightMin:
- Start from the target node.
- Set a "temp" node equal to the target node.
- Move to left of temp node until the left of temp is equal to NULL.
- Finally return temp's value. The code for RightMin -
int RightMin(struct node *root)
{
struct node *temp = root;
while(temp->left != NULL){
temp = temp->left;
}
return temp->data;
}
Algorithm for deletion:
- Start with the root node.
- Check if root value is greater than the node to be deleted. If so, traverse in the left subtree. If not, traverse in the right subtree.
- If the node value is equal to the target value, check if it has zero, one or two child nodes.
- If no child node is there (leaf node (node->left == NULL and node->right == NULL)), free the node itself.
- If one child node is present (node->left == NULL or
node->right == NULL), swap the parent node with the
child node and free the nod. Then return the swapped parent node. - If two child nodes are present, find the rightMin and perform the deletion in the right subtree.
Code for node deletion is -
NODE *deleteNode(NODE *root, int val)
{
if(root == NULL){
printf("Empty Tree!\n");
return NULL;
}
if(root->data < val){
root->right = deleteNode(root->right,val);
}
else if(root->data > val){
root->left = deleteNode(root->left,val);
}
else
{
if(root->left == NULL && root->right == NULL){ // leaf node condition
free(root);
return NULL;
}
else if(root->left == NULL){ // when right child is present
NODE *temp = root->right;
free(root);
return temp;
}
else if(root->right == NULL){ // when left child is present
NODE *temp = root->left;
free(root);
return temp;
}
else{ // when both child nodes are present
int rightMin = RightMin(root->right);
root->data = rightMin;
root->right = deleteNode(root->right,rightMin);
}
}
}
Final Code
#include <stdio.h>
#include <stdlib.h>
typedef struct node{
int data;
struct node *left;
struct node *right;
}NODE;
NODE *createnode(int val){
NODE *newnode = (NODE *)malloc(sizeof(NODE));
newnode->data = val;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
NODE *insertInTree(int val, NODE *root){
NODE *newnode = createnode(val);
if(root == NULL){
root = newnode;
}else{
if(newnode->data <= root->data){
if(root->left == NULL){
root->left = newnode;
}else{
insertInTree(val, root->left);
}
}
else if(newnode->data > root->data){
if(root->right == NULL){
root->right = newnode;
}
else{
insertInTree(val, root->right);
}
}
}
return root;
}
void inorder(NODE *root){
if(root == NULL){
return;
}else{
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
void deleteLeafNode(int val, NODE *root){
if(root == NULL){
printf("Empty Tree!\n");
}else{
if(root->data > val){
//traverse in left subtree
if(root->left->data == val){
//parent node for target found
root->left = NULL;
}else{
deleteLeafNode(val, root->left);
}
}
else if(root->data < val){
//traverse in right subtree
if(root->right->data == val){
//parent node for target found
root->right = NULL;
}else{
deleteLeafNode(val, root->right);
}
}
else{
//root node is the target and root is leaf node.
root = NULL;
}
}
}
int RightMin(struct node *root)
{
struct node *temp = root;
while(temp->left != NULL){
temp = temp->left;
}
return temp->data;
}
NODE *deleteNode(NODE *root, int val)
{
if(root == NULL){
printf("Empty Tree!\n");
return NULL;
}
if(root->data < val){
root->right = deleteNode(root->right,val);
}
else if(root->data > val){
root->left = deleteNode(root->left,val);
}
else
{
if(root->left == NULL && root->right == NULL){ // leaf node condition
free(root);
return NULL;
}
else if(root->left == NULL){ // when right child is present
NODE *temp = root->right;
free(root);
return temp;
}
else if(root->right == NULL){ // when left child is present
NODE *temp = root->left;
free(root);
return temp;
}
else{ // when both child nodes are present
int rightMin = RightMin(root->right);
root->data = rightMin;
root->right = deleteNode(root->right,rightMin);
}
}
}
int main(){
NODE *root = NULL;
int ch;
do{
printf("Enter: \n\t1. Insert\n\t2. Delete\n\t3. Exit\n");
printf("Enter choice: ");
scanf(" %d", &ch);
switch(ch){
case 1:
{
//Insert
printf("Enter value: ");
int val;
scanf(" %d", &val);
root = insertInTree(val, root);
break;
}
case 2:
{
//Delete
printf("Enter value to delete: ");
int val;
scanf(" %d", &val);
printf("Inorder representation before deletion: ");
inorder(root);
root = deleteNode(root, val);
printf("Updated Inorder representation: ");
inorder(root);
break;
}
case 3:
{
//Exit
printf("EXITING...\n");
break;
}
default:
{
printf("Enter Valid Choice!\n");
break;
}
}
}while(ch != 3);
}
Fin.
I hope you liked reading this article and got to learn something from it. You can read my other posts here.
Thanks for reading!
Comments (0)