In this article we're gonna see a basic layout of the Quicksort Algorithm and how we can implement it in C language.
What is Quicksort Algorithm?
It is a simple sorting algorithm that works on Divide and Conquer Strategy. Through this algorithm, we choose a random element from the array and call it the Pivot Element. Then we divide the array such that half the elements(left sub-array) contains elements smaller than the pivot element and the other half(right sub-array) contains elements greater than the pivot element. We keep on dividing the array until the array size becomes so small that they get sorted through this method.
This method of sorting is called "Quick" because the time for sorting is significantly faster than any other sorting method that we've come across so far. It takes O(n*log(n)) time.
The Pivot Element
Pivot element can be chosen at random from the array. In an ideal situation, it is considered to be that element which could be considered to be the middle-most value of all the array element values, i.e, the median value. However, while implementing the logic in the code we usually consider the first or last element of the unsorted array as the pivot element.
The Algorithm
Now, let's get into the algorithm part.
Let's consider that we have an array names "arr" of size "n" and we have to sort it with quicksort. For that, firstly we'll learn about something called Partition Operation.
Partition Operation
Through this operation, we divide the whole array in the given range with respect to the pivot element. Left subarray should contain all the elements smaller than the pivot element, followed by the pivot element, followed by the right subarray containing all elements greater than the pivot elements. Steps for it are as follows:
- Choose a Pivot Element. Here, we'll consider the first element-arr[0] to be the pivot element.
- Let there be an integer left holding the index value of the first element of the array, an integer right holding the index value of the last element of the array and an integer called pivot holding index of pivot element.
- As we've chosen the first element to be the pivot element, left and pivot will point at the same element and right will point at the rightmost element.
- Check if the pivot is equal to the left index or right index.
- if pivot index == left index :
- if the right element is greater than pivot element, move right to the element preceding it(right--).
- Otherwise, swap the left element with the right element. Change the value of pivot to the right index.
- if pivot index == right index :
- if the left element is smaller than pivot element, move left to the next element(left++).
- Otherwise, swap the right element with the left element. Change the value of pivot to the left index.
- Repeat step-4 until the left index becomes greater than or equal to the right index.
- by the time left==right index, all three - pivot, right and left will all point at the same element. That index value becomes the index value of the pivot element in the final sorted array. So, we'll return the value of the pivot variable.
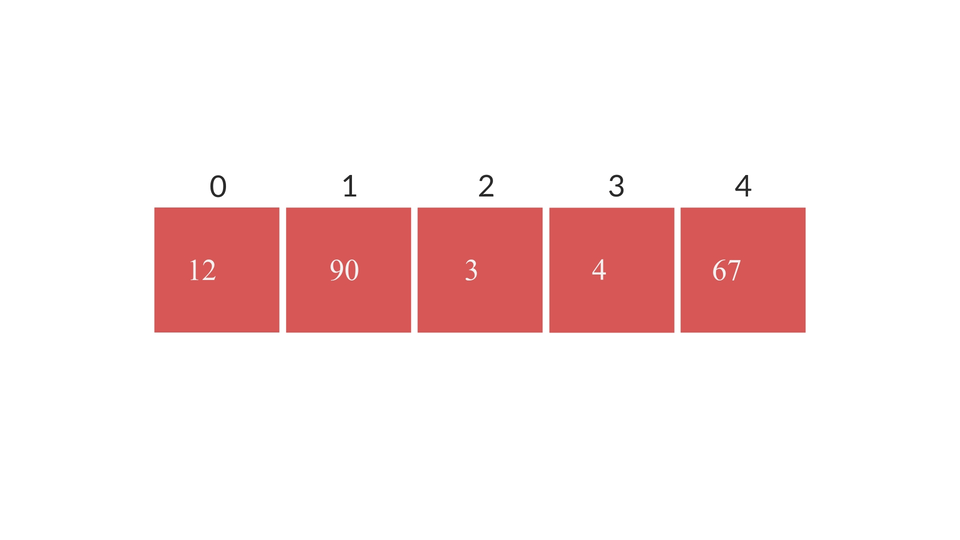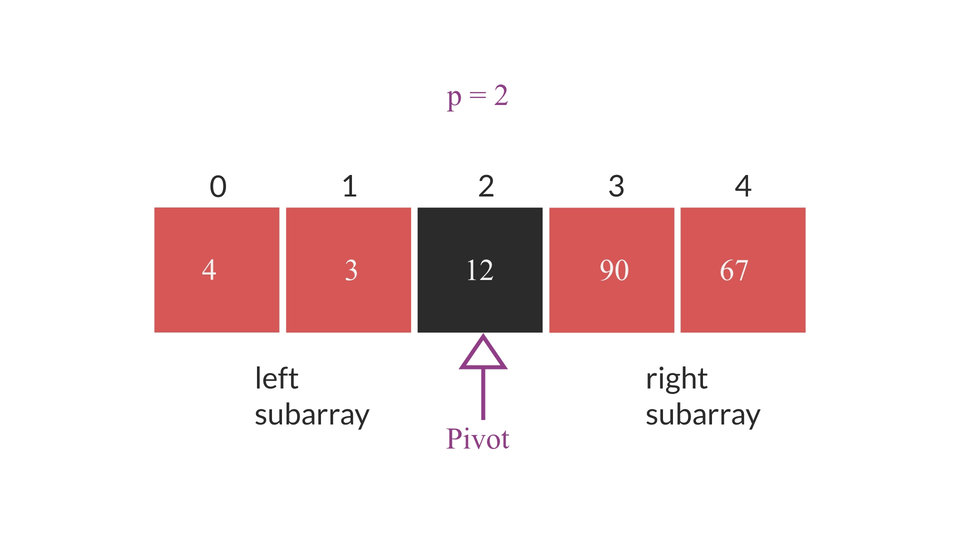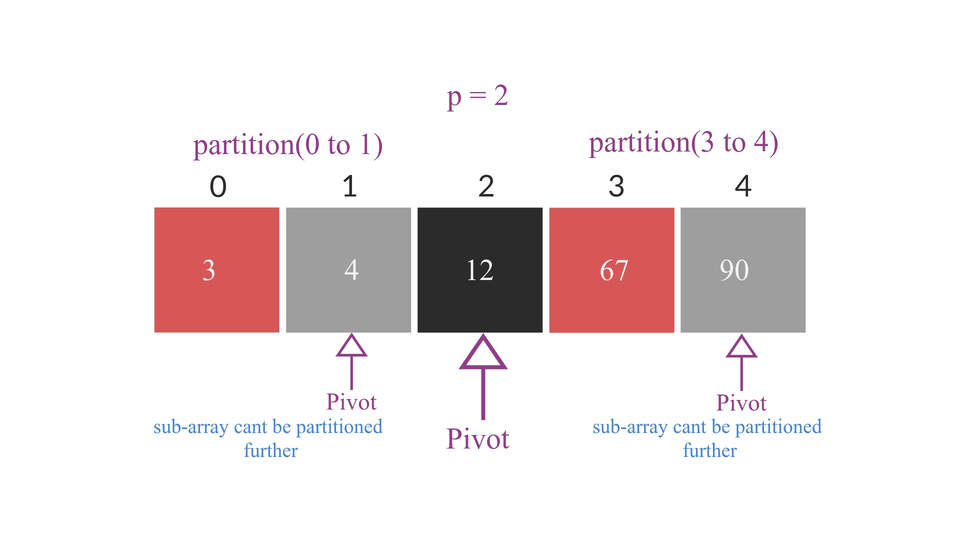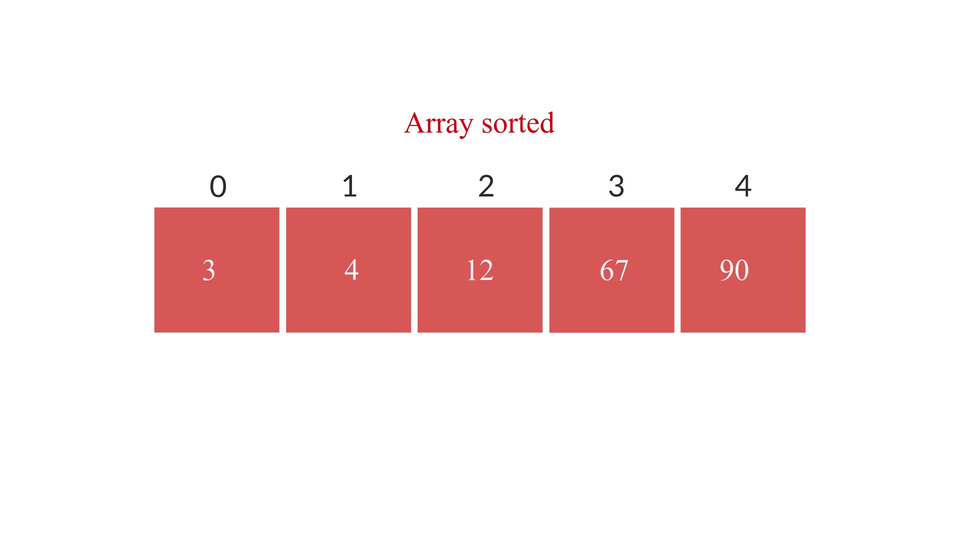
The procedure visually looks something like this -
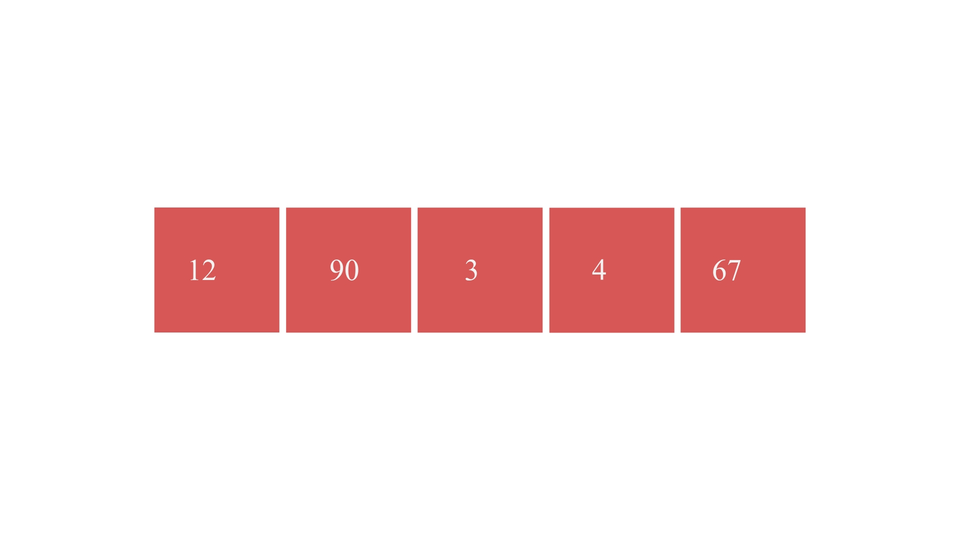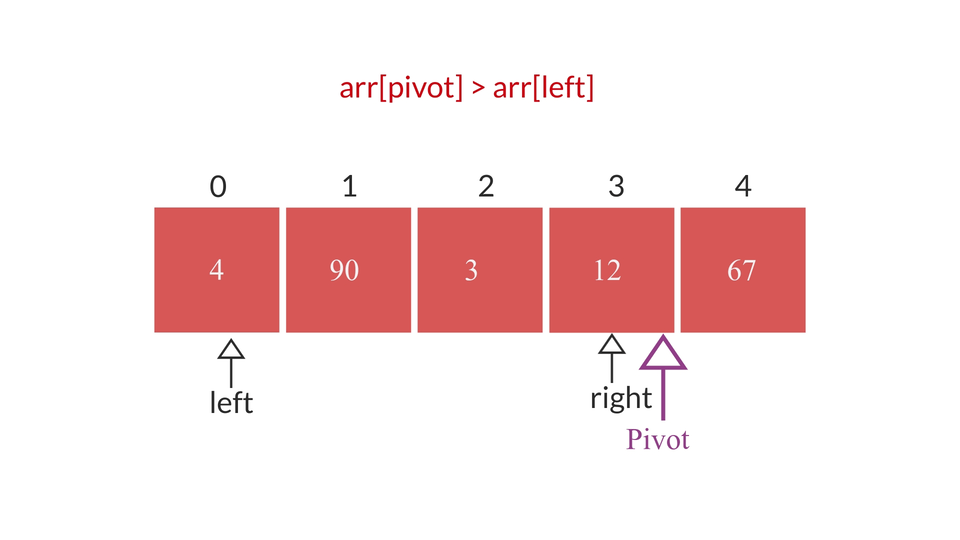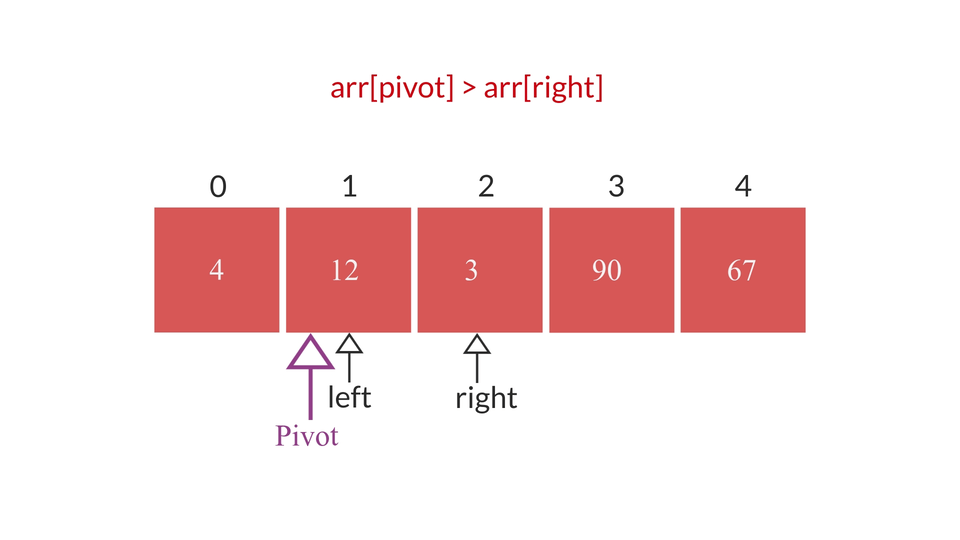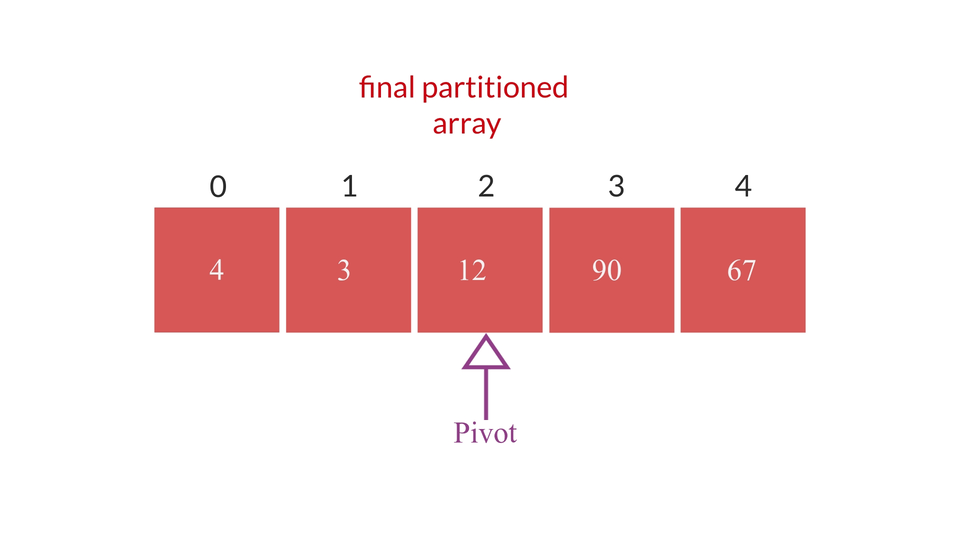
The Quicksort Algorithm
- Firstly, find the pivot index value by running the partition algorithm from 0 to n-1 range. Store the value in a variable. Let's say that variable is "p".
- then run the partition algorithm for subarray from beginning of the array to p-1 index position(0 to p-1).
- then run the partition algorithm for subarray from p+1 index value to end of the array(p+1,n-1).
By the end of the whole process, the partition function would be called again and again until the whole array is sorted.
So, the full algorithm looks something like this -
Code
The C code for partition function is as follows:
View Website
View Website
View Website
int partition(int *arr, int l, int r){
int temp;
int pivot = l; //is the leftmost element
int right = r;
int left = l;
while(left<right){
if(pivot==left){
if(arr[right] <= arr[pivot]){
//swap pivot with the right element
temp = arr[right];
arr[right] = arr[pivot];
arr[pivot] = temp;
pivot = right;
}else if(arr[right] > arr[pivot]){
right--;
}
}else if(pivot == right){
if(arr[left] > arr[pivot]){
//swap pivot with the left element
temp = arr[left];
arr[left] = arr[pivot];
arr[pivot] = temp;
pivot = left;
}else if(arr[left] <= arr[pivot]){
left++;
}
}
}
return pivot;
//by the end of the procedure, the left, right and pivot will all point at the same element.
//all the elements to the right of pivot will be greater than privot element.
// all the elements to the left of pivot will be smaller than it.
}
The C code for quicksort function is -
void quicksort(int *arr, int l, int r){
int low = l;
int high = r;
if(l<r){
int p = partition(arr, low, high);
quicksort(arr, l, p-1);
quicksort(arr, p+1, r);
}
}
And the whole program for it is -
#include <stdio.h>
int partition(int *arr, int l, int r){
int temp;
int pivot = l; //is the leftmost element
int right = r;
int left = l;
while(left<right){
if(pivot==left){
if(arr[right] <= arr[pivot]){
//swap pivot with the right element
temp = arr[right];
arr[right] = arr[pivot];
arr[pivot] = temp;
pivot = right;
}else if(arr[right] > arr[pivot]){
right--;
}
}else if(pivot == right){
if(arr[left] > arr[pivot]){
//swap pivot with the left element
temp = arr[left];
arr[left] = arr[pivot];
arr[pivot] = temp;
pivot = left;
}else if(arr[left] <= arr[pivot]){
left++;
}
}
}
return pivot;
//by the end of the procedure, the left, right and pivot will all point at the same element.
//all the elements to the right of pivot will be greater than privot element.
// all the elements to the left of pivot will be smaller than it.
}
void quicksort(int *arr, int l, int r){
int low = l;
int high = r;
if(l<r){
int p = partition(arr, low, high);
quicksort(arr, l, p-1);
quicksort(arr, p+1, r);
}
}
int main(){
int n;
printf("Enter the number of elements: ");
scanf(" %d", &n);
int arr[n];
printf("Enter the elements of the array: \n");
for(int i=0; i<n; i++){
//getting the elements of the array one by one
printf("Enter element%d: ", i+1);
scanf(" %d", &arr[i]);
}
//printing the unsorted array
printf("UNSORTED ARRAY: ");
for(int i=0; i<n; i++){
printf("%d ", arr[i]);
}
//apply quicksort
quicksort(arr, 0, n-1);
//print the final array-
printf("\nSorted array: ");
for(int i=0; i<n; i++){
printf("%d ", arr[i]);
}
}
Time Complexity
The best and average-case time complexity of Quicksort algorithm is O(n*log(n)). The worst case time complexity is O(n²).
The worst-case time complexity happens if the pivot element is not chosen carefully, instead of being near the median value, it is either the smallest or the largest value, making either the left or right subarray empty and the other subarray contain the remaining n-1 elements.
On the other hand the best-case time complexity is when the chosen pivot element is exactly the median value of all the array elements.
Conclusion
Any program that uses the method of recursion and Divide and Conquer Strategy becomes a little tricky to understand. I hope this post helped you in gaining a little bit clarity about the concept involved in this algorithm. For reading more such articles, you can visit this link.
Thanks for reading!🤩
Comments (0)