In this article I'm gonna talk about the ways of traversal we can perform on Binary Trees.
A node of a binary tree primarily consists of three components -
- it's own data (D)
- It's left child (L)
- It's right child (R)
Consider a node to be the most basic unit of a binary tree. Then the traversal methods that can be performed on a tree are nothing but permutations of the three above listed components. The permutations can be -
- D, L, R
- D, R, L
- L, D, R
- L, R, D
- R, L, D
- R, D, L
But there are some constraints to the traversal methods. Left child(L) should always come before the right child(R). So the permutations that we'll use are -
- D, L, R
- L, D, R
- L, R, D
So, the three ways of traversal are -
- Preorder Traversal - (D, L, R) type permutation. In this type of traversal, we visit the parent node first, then the left child node and then the right child node.
- Inorder Traversal - (L, D, R) type permutation. In this type of traversal, we visit the left child, then the parent node and then the right child.
- Postorder Traversal - (L, R, D) type permutation. In this type of traversal, visit the left child, then the right child and then the parent node.
Let's now look at the code for the three methods of traversal.
Preorder Traversal
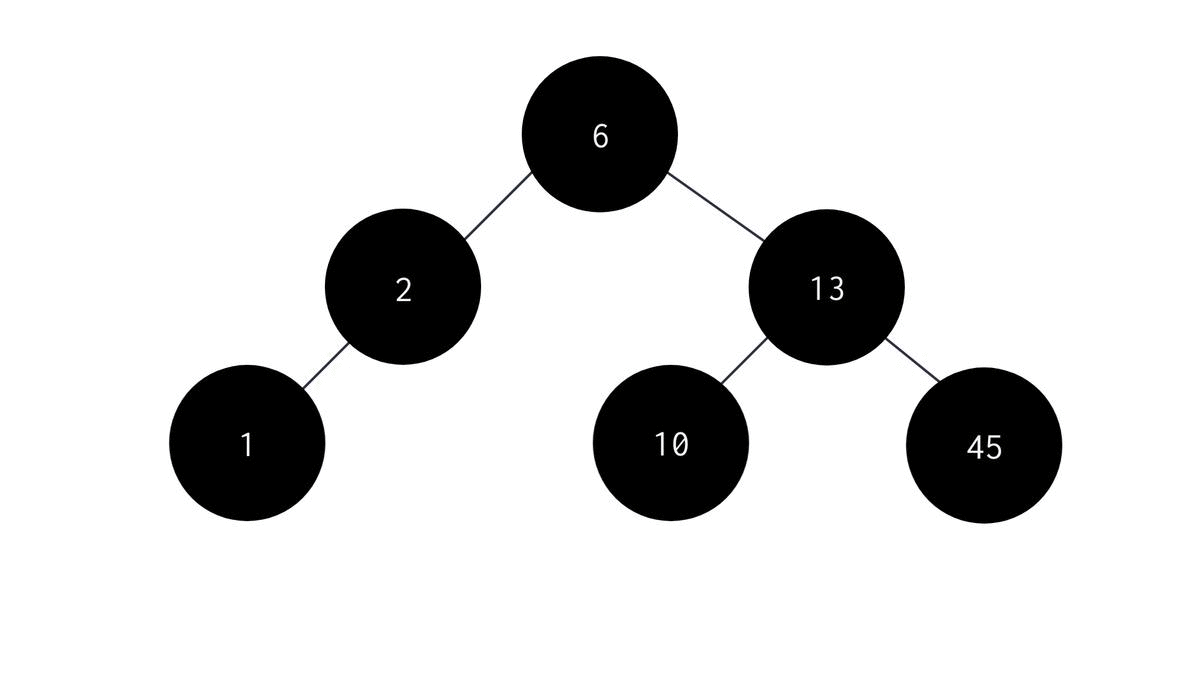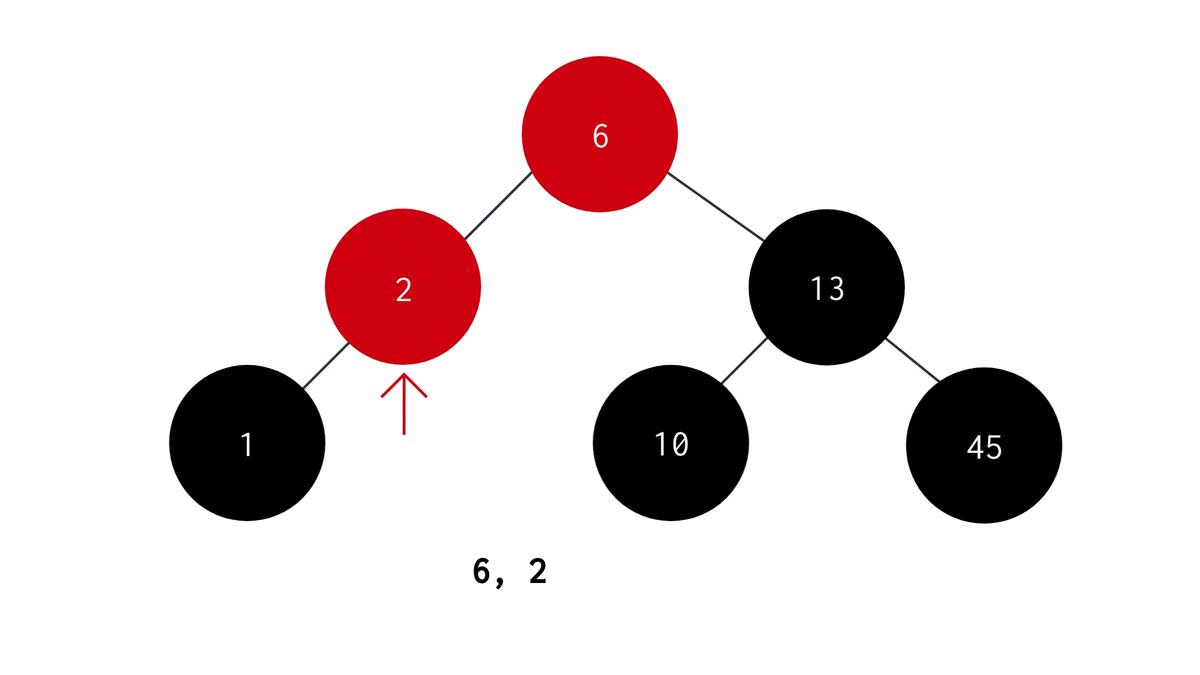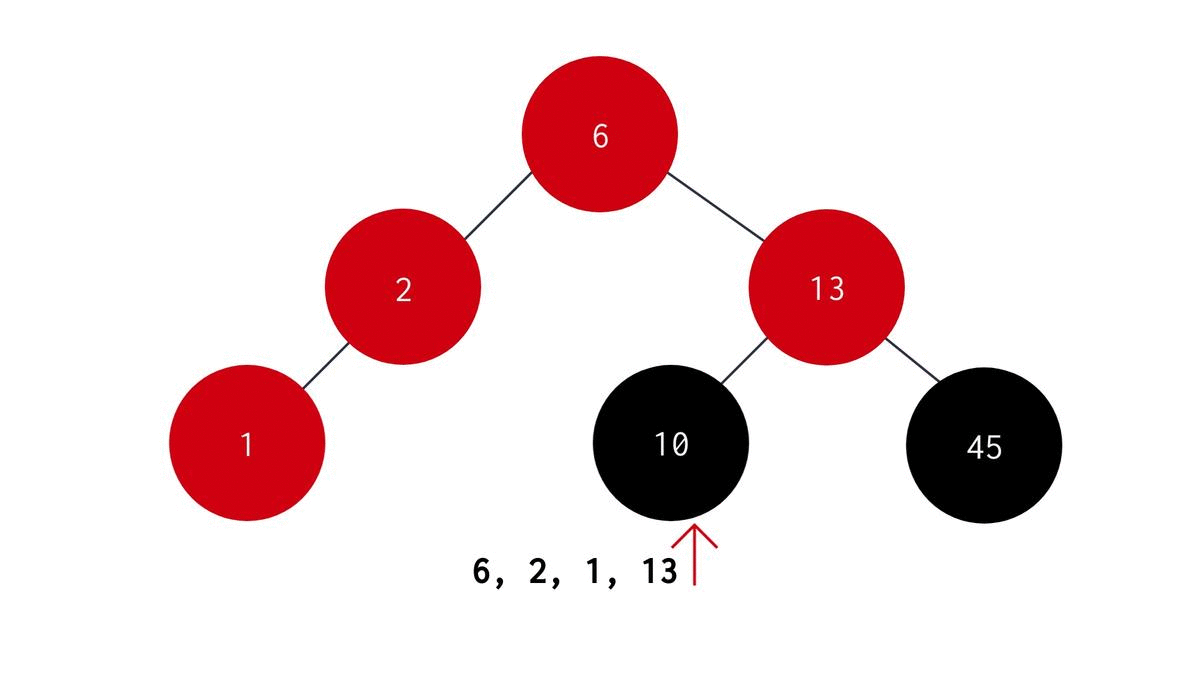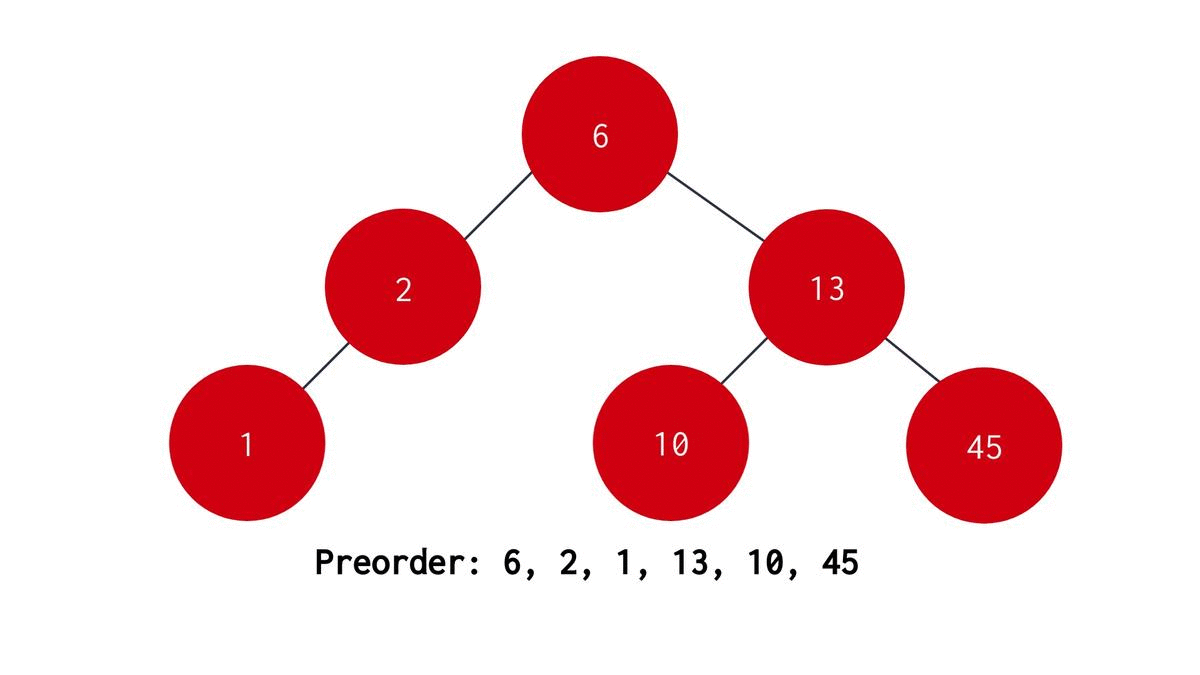
In preorder Traversal we first visit the parent node, then the left child node and finally the right child node. The algorithm for Preorder recursive function is as follows -
- Start with the root node as parent node.
- Print the value stored in the parent node.
- Recursively visit the left subtree to the parent node.
- Recursively visit the right subtree to the parent node. The C code for the same is :
void preorder(NODE *root){
if(root == NULL)return;
else{
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}
}
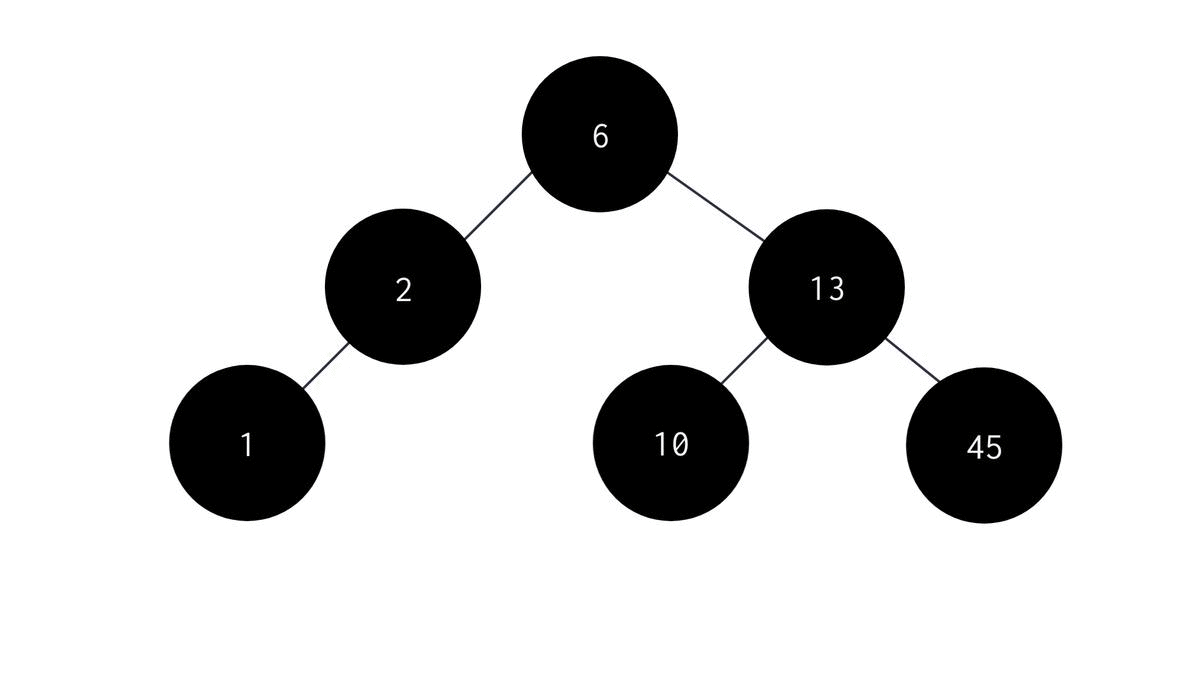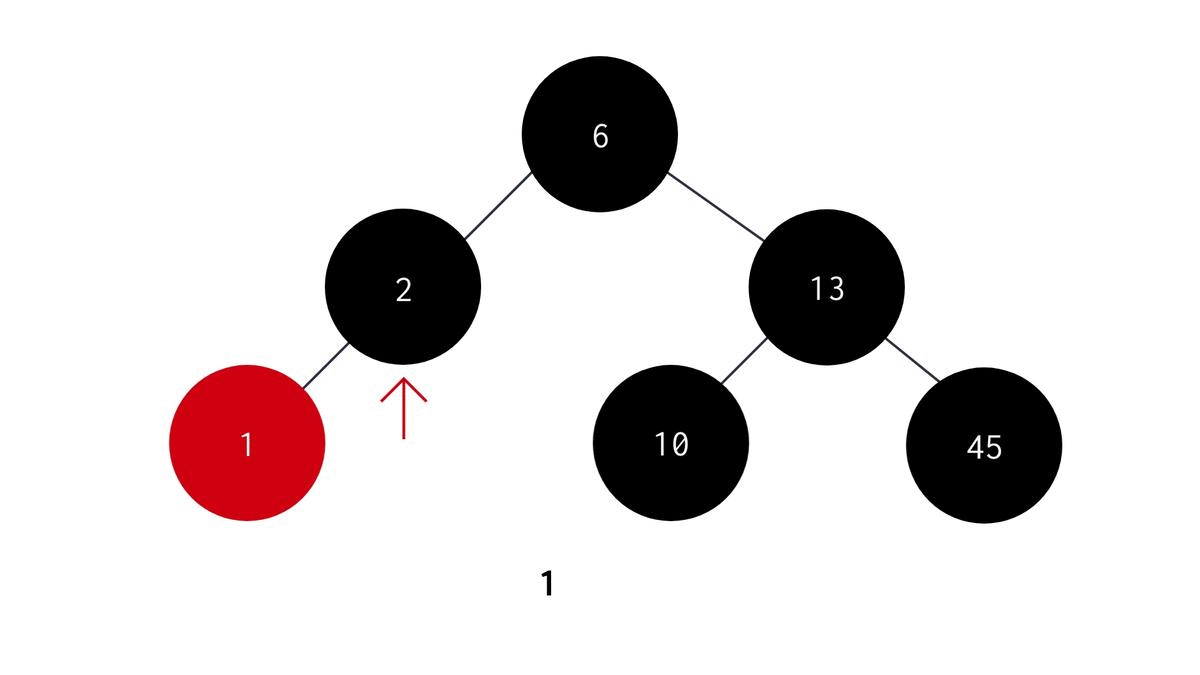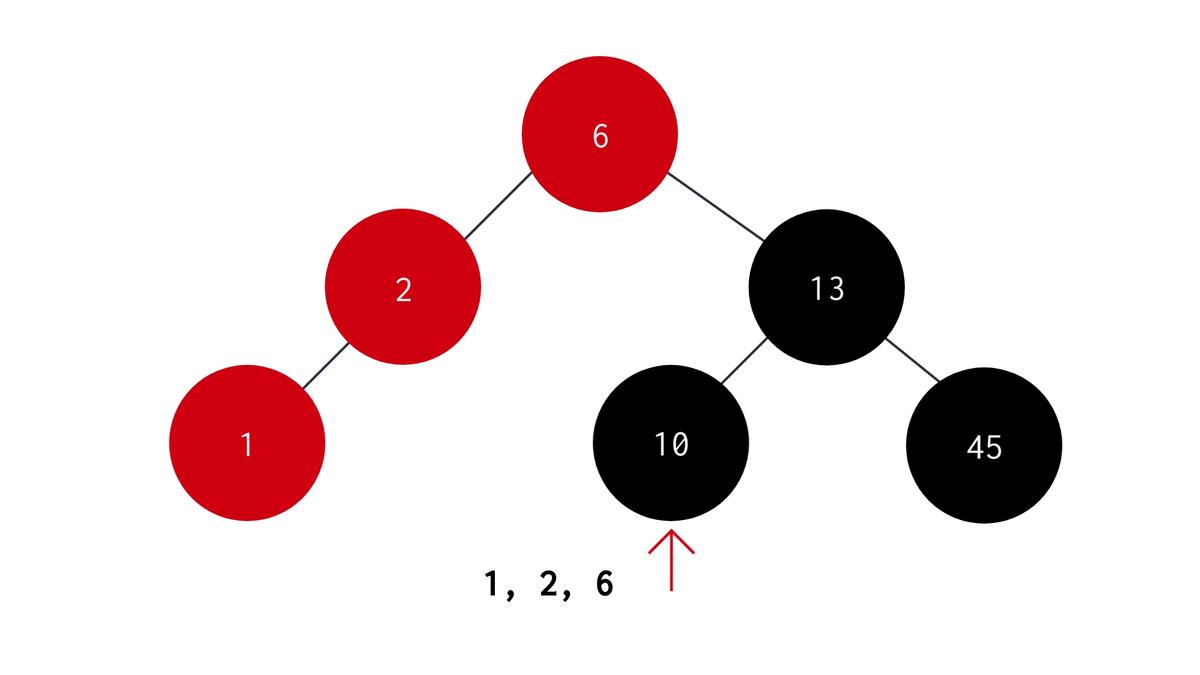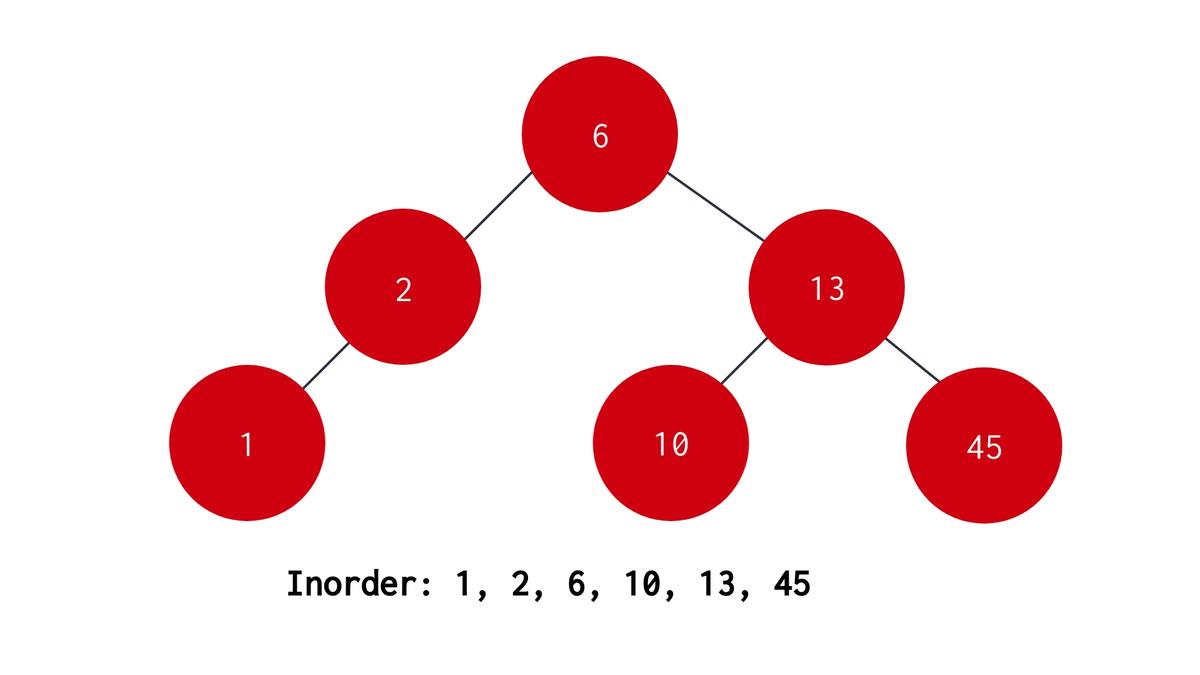
Inorder Traversal
In Inorder Traversal, we first visit the left child node, then visit the parent node and finally visit the right child node. The algorithm for recursive Inorder Traversal is:
 View Website
View Website
 View Website
View Website
 View Website
View Website
- Start with the root node as the parent node.
- Recursively visit the left subtree to the parent node.
- Print the data stored in the parent node.
- Recursively visit the right subtree to the parent node. The C code for the same is :
void inorder(NODE *root){
if(root == NULL){
return;
}else{
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
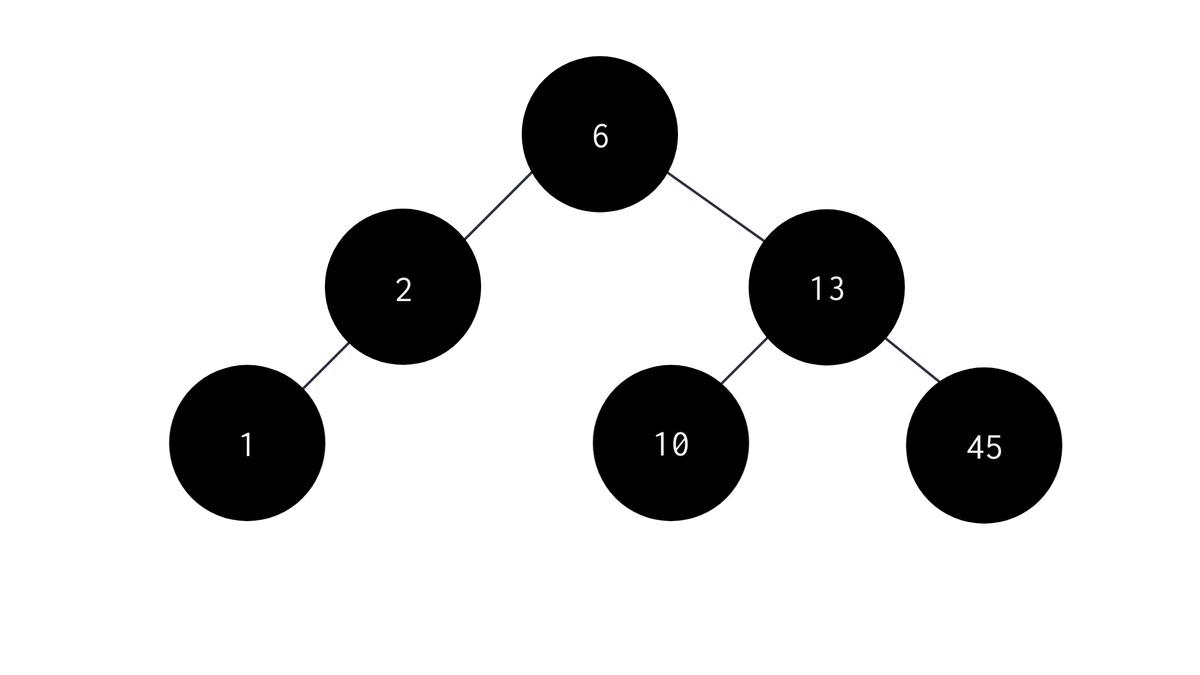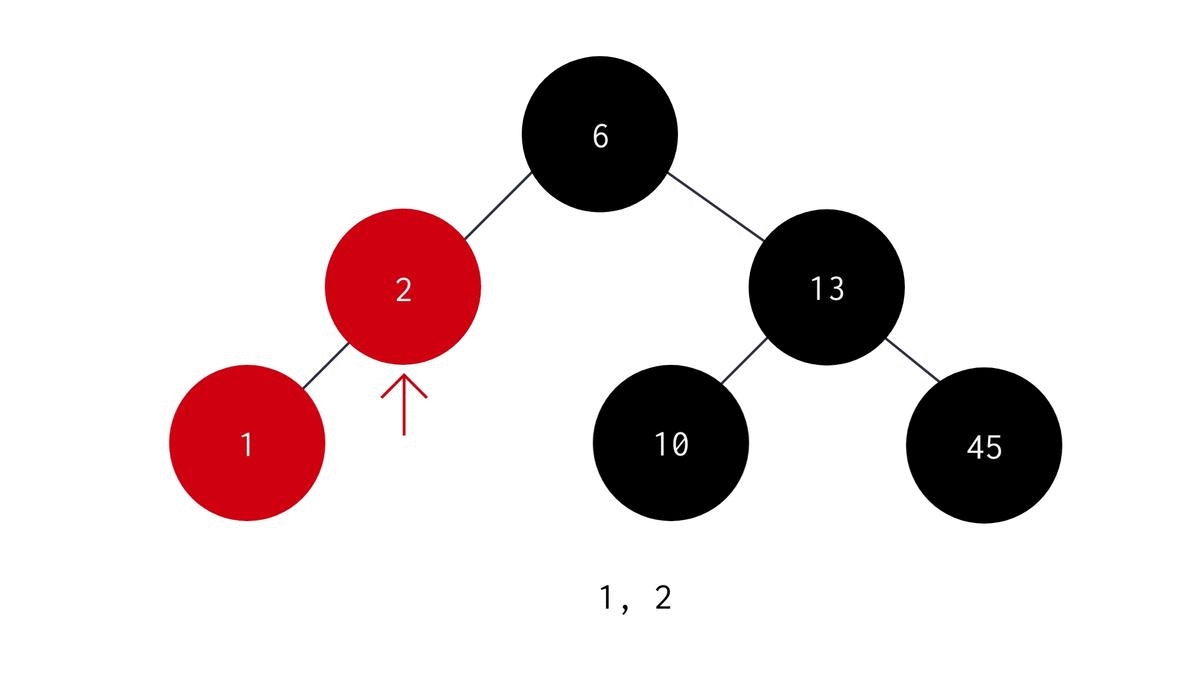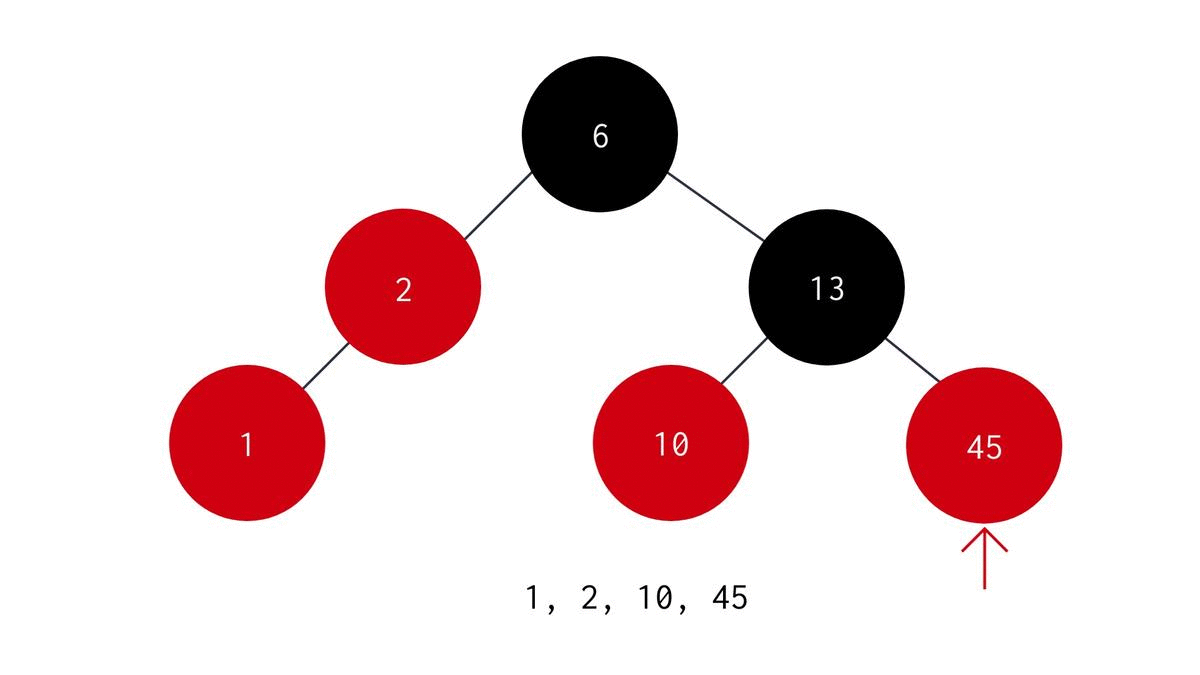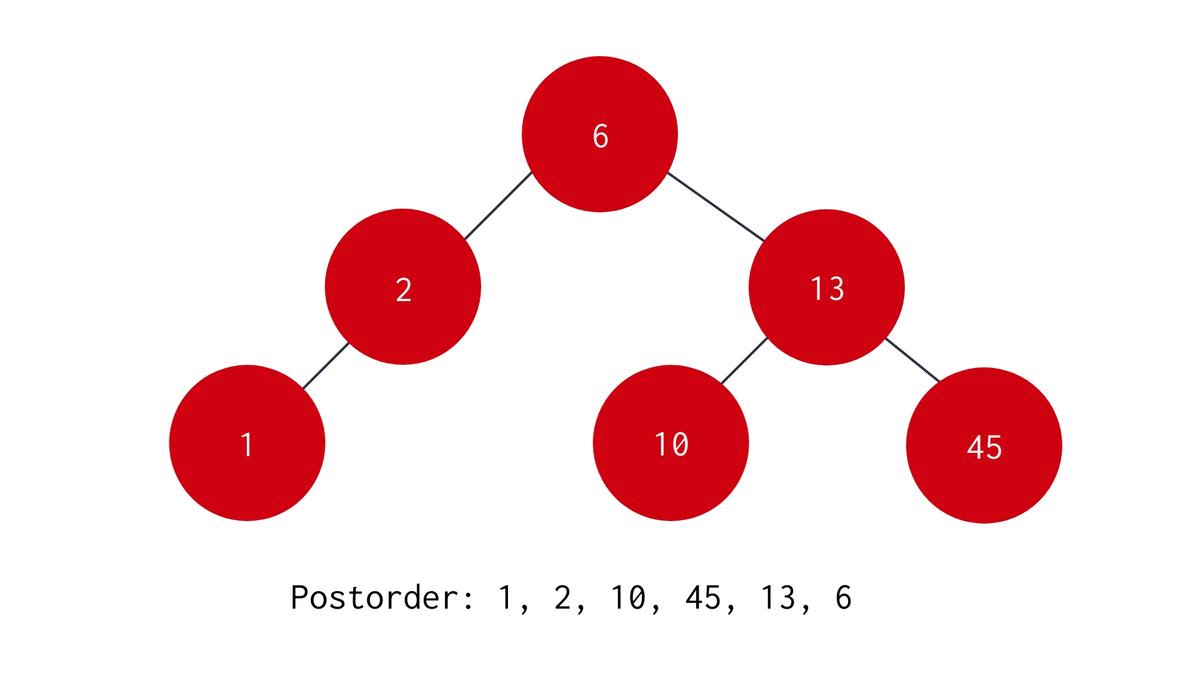
Postorder Traversal
In Postorder Traversal we visit the left child node, then visit the right child node and finally visit the parent node. The algorithm is :
- Start with the root node as the parent node.
- Recursively visit the left subtree to the parent node.
- Recursively visit the right subtree to the parent node.
- print the data stored in the parent node. The C code for the same is:
void postorder(NODE *root){
if(root==NULL)return;
else{
postorder(root->left);
postorder(root->right);
printf("%d ", root->data);
}
}
Full Code
The full code to perform all the three methods -
#include <stdio.h>
#include <stdlib.h>
typedef struct node{
int data;
struct node *left;
struct node *right;
}NODE;
NODE *createnode(int val){
NODE *newnode = (NODE *)malloc(sizeof(NODE));
newnode->data = val;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
NODE *insertInTree(int val, NODE *root){
NODE *newnode = createnode(val);
if(root == NULL){
root = newnode;
}else{
if(newnode->data <= root->data){
if(root->left == NULL){
root->left = newnode;
}else{
insertInTree(val, root->left);
}
}
else if(newnode->data > root->data){
if(root->right == NULL){
root->right = newnode;
}
else{
insertInTree(val, root->right);
}
}
}
return root;
}
void preorder(NODE *root){
if(root == NULL)return;
else{
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}
}
void inorder(NODE *root){
if(root == NULL){
return;
}else{
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
void postorder(NODE *root){
if(root==NULL)return;
else{
postorder(root->left);
postorder(root->right);
printf("%d ", root->data);
}
}
int main(){
NODE *root = NULL;
int ch;
do{
printf("Enter: \n\t1. Insert\n\t2. Preorder Traversal\n\t3. Inorder Traversal\n\t4. Postorder Traversal\n\t5. Exit\n");
printf("Enter choice: ");
scanf(" %d", &ch);
switch(ch){
case 1:
{
//Insert
printf("Enter value: ");
int val;
scanf(" %d", &val);
root = insertInTree(val, root);
break;
}
case 2:
{
//Preorder
printf("Preorder Traversal: ");
preorder(root);
printf("\n");
break;
}
case 3:
{
//Inorder
printf("Inorder Traversal: ");
inorder(root);
printf("\n");
break;
}
case 4:
{
//Postorder
printf("Postorder Traversal: ");
postorder(root);
printf("\n");
break;
}
case 5:
{
//Exit
printf("EXITING...\n");
break;
}
}
}while(ch!=5);
}
Applications
Traversal methods in Binary Tree is one of the most important topics. It is most commonly used in generating prefix, infix and postfix notations. While infix notation is more human friendly, prefix and postfix notations are preferred for machines as they're easily parseable and the complexity of the problem also reduces significantly. Such Trees are also known as "Expression Trees".
Fin.
I hope you liked reading this article. You can find my other posts here
Happy Learning!


Comments (0)