Sorting means to arrange a group of things in a specific order. Algorithms that help us sort a group of items are called Sorting Algorithms. In this article I'm gonna give a brief introduction about Sorting Algorithms and its various types that you might come across.
What are Sorting Algorithms?
They're nothing but just a way to sort a group of items in a particular order.
Imagine that you're scrolling through a shopping website searching for a specific item. You apply a filter on the search results such that it only shows you the items in increasing order of the prices. Which algorithm do you think was used in producing those results? Sorting Algorithms!
Types of Sorting Algorithms
There are many different types of Sorting Algorithms. One can apply these algorithms based on the type of problem they encounter and the time and space complexity best suited for that problem. Following I've listed some algorithms that you might come across most oftenly.
Bubble Sort
This is the simplest sorting algorithm. According to this algorithm, adjacent pair of elements are swapped if they're present in the wrong order repeatedly until all the elements are arranged correctly.
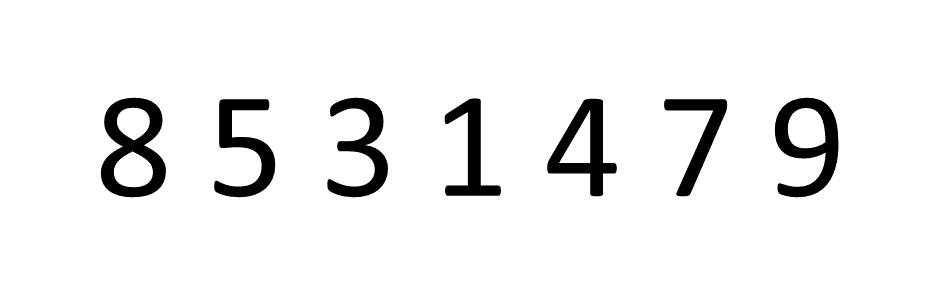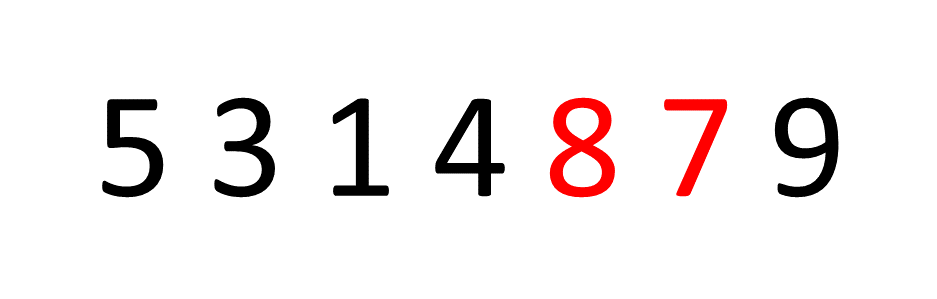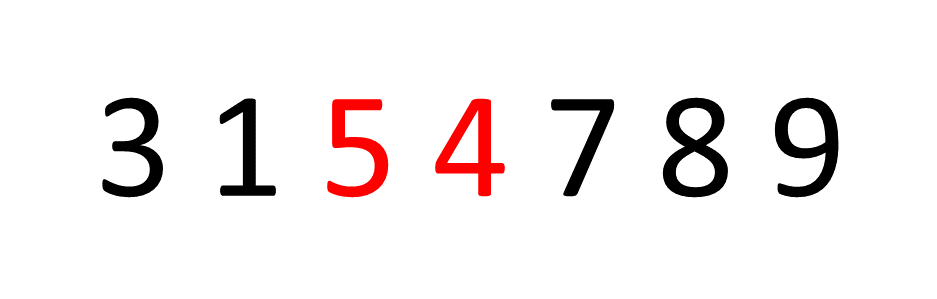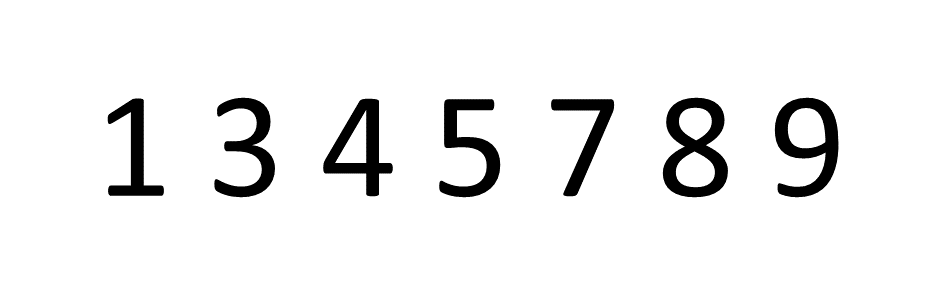The movement of array elements is compared with the movement of an air bubble in water. Just like how an air bubble floats up towards the water surface, the smallest/largest(based on the ordering condition) element moves to the end of the array by the end of the execution of the algorithm.
Selection Sort
In this algorithm, the smallest element is searched, when that element is found - it is placed at the beginning of the array. Repeatedly, smallest element is picked up from the unsorted part and queued in the sorted half of the array.
In each step the smallest element is selected, hence the name "Selection" Sort.
Insertion Sort
In this algorithm, elements from the unsorted array are chosen and placed at their correct positions in the sorted half.
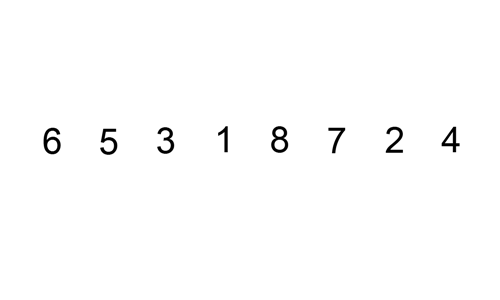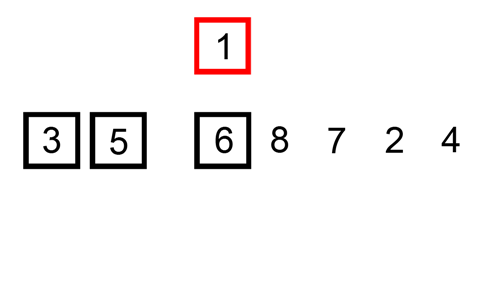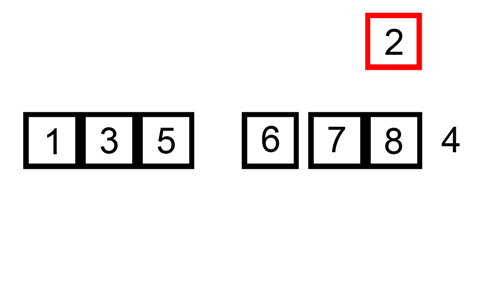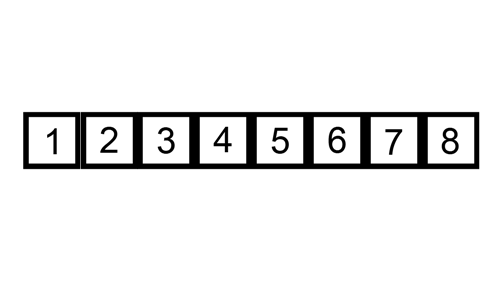As each element is inserted in the sorted part of the array, this algorithm is called "Insertion Sort".
Merge Sort
In this algorithm, an array is repeatedly divided in two equal halves until all the resulting halves contain only one element at the end. Then these halves are merged step by step with each other in the right order of their values, reforming the array but in a sorted order.
View Website
View Website
View Website
This is an example of Divide and Conquer Algorithm. In these type of algorithms a big problem is divided into smaller problems until they become so small that they can be solved with the most simple logic.
Merge Sort is considered to be the fastest sorting algorithm.
As the sub-arrays are merged to form the sorted array, this sorting algorithm is called Merge Sort.
Quick Sort
This is another example of Divide and Conquer Algorithm.
In this algorithm, an element is picked up and is called Pivot Element. Then the array is arranged such that all elements smaller than the pivot element are placed to its left and the larger ones are placed to its right. Then the array with smaller and larger values are divided and these steps are repeated in each of the sub-arrays until only one element is left. Then these single elements are merged back into the array according to their positions from left to right.
Lastly, this algorithm is called "Quick" Sort as it proves to be asymptotically faster than the other sorting algorithms(in some cases faster than even Merge Sort). Moreover, it doesn't require extra memory for its execution.
This is what it looks like -
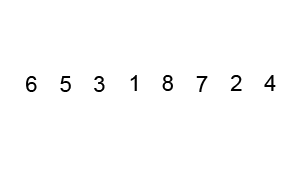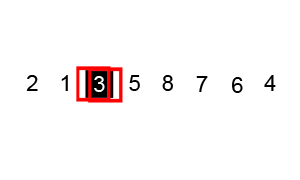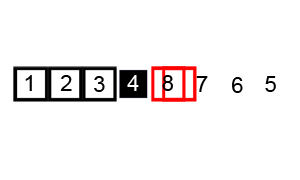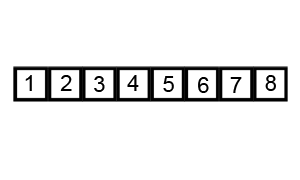
Counting Sort
In this algorithm, elements are sorted based on their frequency in the array. The new positions of the elements are mapped out using an auxiliary array.
Conclusion
There are a number of sorting algorithms. The ones I've listed above are the most common and basic ones. Hope you got some idea about these sorting algorithms and you liked reading this article.
Thanks for reading!😊
Comments (0)